Hình chóp tam giác đều S.ABC có AC=6cm. Gọi O là giao điểm ba đường trung tuyến của đáy ABC, SO=2√6cm. Độ dài cạnh bên SB=....cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 7 2023
\(BO=CO=AO=\dfrac{6\sqrt{3}}{3}=2\sqrt{3}\left(cm\right)\)
\(SB=\sqrt{SO^2+OB^2}=\sqrt{24+12}=6\left(cm\right)\)
1 tháng 7 2023
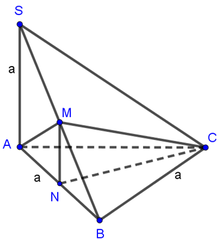
a:ΔSBC cân tại S có SM là trung tuyến
nên SM vuông góc BC
BC=6cm
=>BM=CM=3cm
SM=căn 5^2-3^2=4cm
Sxq=5*3/2*4=5*3*2=30cm2
Stp=30+5^2*căn 3/2=(60+25căn 3)/2cm2
b: BC vuông góc SM
BC vuông góc AM
=>BC vuông góc (SAM)
CM
17 tháng 2 2019
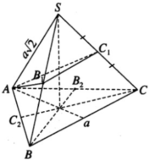
Gọi giao điểm thứ hai của mặt cầu với đường thẳng SA là D, ta có:
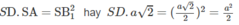
Do đó
20 tháng 5 2017
Do đó, \(SD=\dfrac{a^2}{2}:a\sqrt{2}=\dfrac{a\sqrt{2}}{4}\)
và \(AD=SA-SD=\dfrac{3a\sqrt{2}}{4}\)
CM
17 tháng 10 2019
Đáp án D
Gọi d là tiếp tuyến của (C) tại điểm A(1:0).
Ta có: y ' = 3 x 2 − 6 x ⇒ y ' 1 = 3.
Suy ra: d : − 3 x − 1 + 0 ⇔ y = − 3 x + 3.
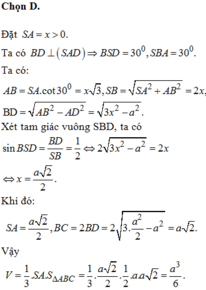
Tính bán kính đường tròn đi qua các đỉnh của mặt đáy?