BÀI TOÁN LỚP 7 CHO TAM GIÁC VUÔNG TẠI A CÓ ĐƯỜNG CAO AH, TRÊN AC LẤY MỘT ĐIỂM K BẤT KỲ. GỌI D LÀ HÌNH CHIẾU CỦA A TRÊN BK. CHỨNG MINH GÓC BDH BẰNG GÓC C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài của em bị sai
Hai tam giác BHD và BKC đồng dạng do chung góc \(\widehat{KBC}\) và \(\widehat{BDH}=\widehat{BCK}\) (cùng bằng \(\widehat{BAH}\))
Do đó tỉ số đồng dạng 2 tam giác là \(k=\dfrac{BD}{BC}\)
\(\Rightarrow\dfrac{S_{BDH}}{S_{BKC}}=k^2=\dfrac{BD^2}{BC^2}\)
Nếu đề bài đúng thì đồng nghĩa ta phải chứng minh:
\(\dfrac{BD^2}{BC^2}=\dfrac{cos^2\widehat{ABD}}{4}=\dfrac{\left(\dfrac{BD}{AB}\right)^2}{4}=\dfrac{BD^2}{4AB^2}\)
\(\Rightarrow BC^2=4AB^2\) nhưng điều này rõ ràng ko đúng (vì đề bài ko hề cho BC=2AB)

a: CH=8-2=6(cm)
\(AB=\sqrt{BH\cdot BC}=4\left(cm\right)\)
\(AC=4\sqrt{3}\left(cm\right)\)
\(AH=4\cdot\dfrac{4\sqrt{3}}{8}=2\sqrt{3}\left(cm\right)\)

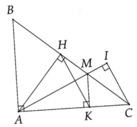
a)
Ta có: ΔABC cân tại A(gt)
mà AM là đường phân giác ứng với cạnh đáy BC(gt)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
\(\Leftrightarrow AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(cmt)
BK là đường cao ứng với cạnh AC(Gt)
AM cắt BK tại I(Gt)
Do đó: I là trực tâm của ΔBAC(Tính chất ba đường cao của tam giác)
Suy ra: CI\(\perp\)AB(Đpcm)

a) Tam giác ABC cân tại A có AM là phân giác, do đó AM cũng là đường cao
AM vuông góc với BC
Lại có BK vuông góc với AC
Do đó I là trực tâm của tam giác ABC
Vậy CI vuông góc với AB
b) Tam giác BDH = tam giác DBP (ch.gn)
Do đó BH = DP
BDKQ là hình chữ nhật => DP = HK
=> BK = BH + HK = DP + DQ (đpcm)

Không mất tính tổng quát, ta xét M thuộc HC (trường hợp M thuộc HB tương tự)
Tam giác ABC vuông tại A có đường cao AH xuất phát từ đỉnh A nên \(AH=\frac{1}{2}BC\) (1) và AH cũng là đường trung tuyến \(\Rightarrow HC=HB=\frac{1}{2}BC\) (2) và đường phân giác => ^CAH = ^BAH. Từ (1) và (2) suy ra \(\Delta\)AHC vuông cân tại H. Từ đó
AH = HC và ^ACH = ^HAC = ^BAH. Tới đây tìm cách chứng minh AI = CK(mình chưa biết làm đâu:v). Từ đó suy ra \(\Delta\)HIA = \(\Delta\)HKC. Suy ra ^AHI = ^CHK suy ra ^IHK = ^IHA + ^AHK = ^CHK + ^AHK = 90o => \(\Delta\)IHK vuông tại H (3)
Mặt khác từ \(\Delta\)HIA = \(\Delta\)HKC suy ra HI =HK suy ra \(\Delta\)IHK cân tại H (4)
Từ (3) và (4) suy ra đpcm.
P/s: Ko chắc, bác zZz Cool Kid zZz check giúp:v

a: Xét ΔABC có
AM,BK là đường cao
AM cắt BK tại I
=>I là trực tâm
=>CI vuông góc AB tại N
b:
Xet ΔAKB vuông tại K và ΔANC vuông tại N có
AB=AC
góc KAB chung
=>ΔAKB=ΔANC
=>BK=CN
DP//NC
=>DP/NC=BD/BC
=>DP/BK=BD/BC
DQ//BK
=>DQ/BK=CD/CB
=>DQ+DP=BK(BD/BC+CD/CB)=BK