Cho nửa đường tròn đường kính AB, gọi M là điểm chính giữa
cung AB. Trên cung AM lấy N, trên tia đối của tia MA lấy điểm D
sao cho MD = MB, trên tia đối của tia NB lấy điểm E sao cho NA
bằng NE, trên tia đối của tia MB lấy C sao cho MC = MA. Chứng
minh 5 điểm A, B, C, D, E cùng thuộc 1 đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

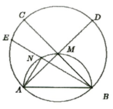
Các tam giác ∆ANE, ∆AMC và ∆BMD vuông cân
=> A E B ^ = A D B ^ = A C B ^ = 45 0
Mà AB cố định nên các điểm A, B, C, D, E cùng thuộc một đường tròn

a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//CD
c: Xét tứ giác ABCE có
N là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//EC
=>C,E,D thẳng hàng

a: Xét ΔAMB và ΔDMC có
MA=MD
góc AMB=góc DMC
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
Do đó: ABDC là hình bình hành
=>BD//AC
c: Xét tứ giác ACBE có
N là trung điểm chung của AB và CE
Do đó: ACBE là hình bình hành
=>BE//AC và BE=AC
ACDB là hình bình hành
=>AC//BD và AC=BD
AC//BD
AC//BE
BD cắt BE tại B
Do đó: D,B,E thẳng hàng
mà BD=BE(=AC)
nên B là trung điểm của DE

b: Xét tứ giác AEBC có
N là trung điểm của BA
N là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE//BC

Đây nhé bạn!!!!
a) Xét tam giác ANE và tg BNC có
góc ẢNE= góc BNC( đối đỉnh )
BN=NE ( gt)
AN=NC( N td AC)
suy ra tg ANE= góc BNC ( c.g.c)
suy ra góc AEN = góc NBC( hai góc tuơng ứng)
suy ra AE//BC( hai góc slt) (1)
Xét tg DAM và tg CBM có
góc DAM= góc CMB
AM=BM (M td AB)
DM=MC( GT)
Suy ra tg DAM= tg CMB( C.g.c)
suy ra góc ADM= góc MCB( hai góc t/ư)
Suy ra DA//BC( hai góc so le trong) (2)
Từ (1) và (2) suy ra D,A,E thẳng hàng( tiên đề Ơ-clít)
b)Xét tam giác ABC có AM=BM(gt)
AN=NC(gt)
suy ra MN là đuơng trung bình tam giác ABC SUy ra MN//BC
MN=1/2 BC
MÀ DE // BC(cmt) suy ra MNED là hình thang
Ta lại có AE=BC(tg ANE=tg BNC)
AD= BC(TG ADM=tg MCB)
suy ra AE+AD=2bc
suy ra DE=2BC
mà MN=1/2 BC
SUY ra MN=1/4DE