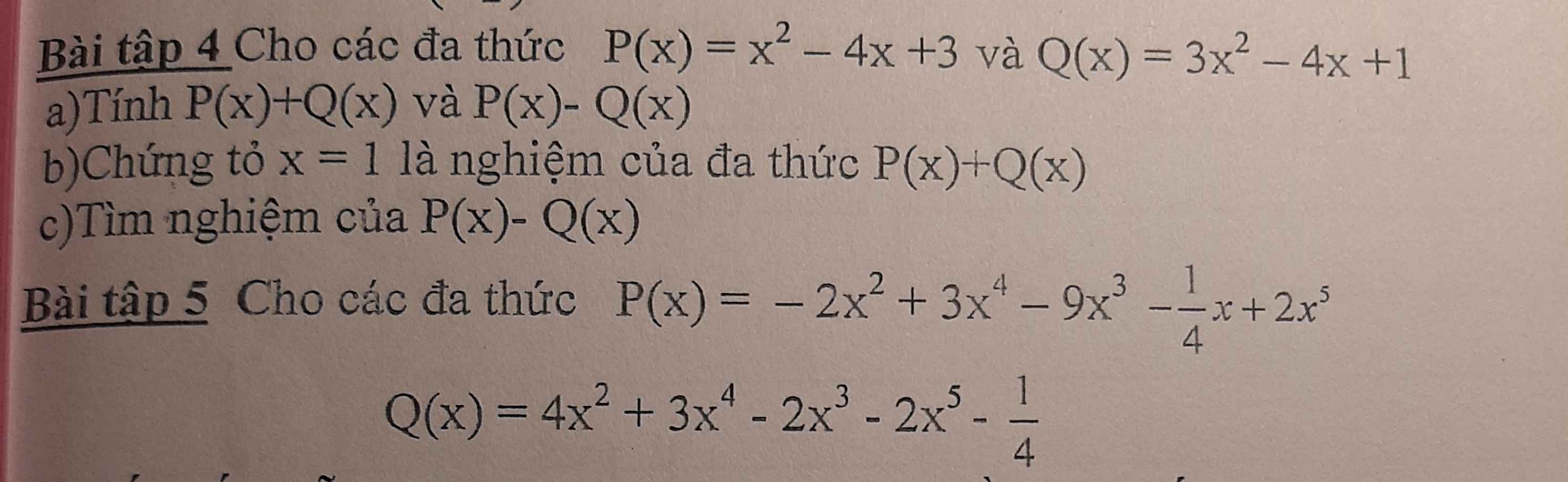Giải giúp mình bài 4 với ạ!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YH
0
YH
0
3T
1
18 tháng 6 2023
4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
17 tháng 4 2021
a, Ta có : \(P\left(x\right)+Q\left(x\right)=x^2-4x+3+3x^2-4x+1=4x^2-8x+4\)
\(P\left(x\right)-Q\left(x\right)=x^2-4x+3-3x^2+4x-1=-2x^2+2\)
17 tháng 4 2021
b, Vì x = 1 là nghiệm của P(x) + Q(x) nên
Thay x = 1 vào P(x) + Q(x) ta được
\(4-8+4=0\)* đúng *
NH
0
21 tháng 7 2021
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=\dfrac{81}{4}+36=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\dfrac{81}{4}}{\dfrac{15}{2}}=\dfrac{27}{10}\)cm
=> \(CH=BC-BH=\dfrac{15}{2}-\dfrac{27}{10}=\dfrac{24}{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}\)
\(=\dfrac{4,5.6}{\dfrac{15}{2}}=\dfrac{18}{5}\)cm
AT
21 tháng 7 2021
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=\left(4,5\right)^2+6^2=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}=7,5\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\left(4,5\right)^2}{7,5}=\dfrac{27}{10}=2,7\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{6^2}{7,5}=\dfrac{24}{5}=4,8\left(cm\right)\)
