3 lớp 7A,7B,7C tham gia phong trào trồng cây xanh bảo vệ môi trường do nhà trường phát động, số cây trồng được của 3 lớp 7A,7B,7C lần lượt tỉ lệ với 2;4;5 biết số cây trồng được của lớp 7C hơn số cây trồng được lớp 7A là 105 cây. tính số cây trồng được của mỗi lớp lần lượt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số cay lớp 7A,7B,7C lần lượt là a,b,c(cây;a,b,c∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{7}=\dfrac{b}{8}=\dfrac{c}{9}=\dfrac{a+b+c}{7+8+9}=\dfrac{120}{24}=5\\ \Leftrightarrow\left\{{}\begin{matrix}a=35\\b=40\\c=45\end{matrix}\right.\)
Vậy ...
gọi số cây 3 lớp 7a,7b,7c trồng đc lần lượt là a,b,c
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{7}=\dfrac{b}{8}=\dfrac{c}{9}\\a+b+c=120\end{matrix}\right.\)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{7}=\dfrac{b}{8}=\dfrac{c}{9}=\dfrac{a+b+c}{7+8+9}=\dfrac{120}{24}=5\)
\(\dfrac{a}{7}=5\Rightarrow a=35\\ \dfrac{b}{8}=5\Rightarrow b=40\\ \dfrac{c}{9}=5\Rightarrow c=45\)

Gọi số cây 7A,7B,7C trồng đc lần lượt là a,b,c(cây;a,b,c∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{8}=\dfrac{a+b+c}{4+6+8}=\dfrac{180}{18}=10\\ \Rightarrow\left\{{}\begin{matrix}a=40\\b=60\\c=80\end{matrix}\right.\)
Vậy ...
Gọi số cây lớp 7A,7B,7C trồng được lần lượt là : a,b,c ( a,b,c thuộc N* )
Do số cây trồng được 3 lớp 7A,7B,7C tỉ lệ với 4,6,8 nên ta có :
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{8}=\dfrac{a+b+c}{4+6+8}=\dfrac{180}{18}=10\) ( t/c dãy tỉ số bằng nhau )
=> a = 10 . 4 = 40 cây
b = 10 . 6 = 60 cây
c = 10 . 8 = 80 cây

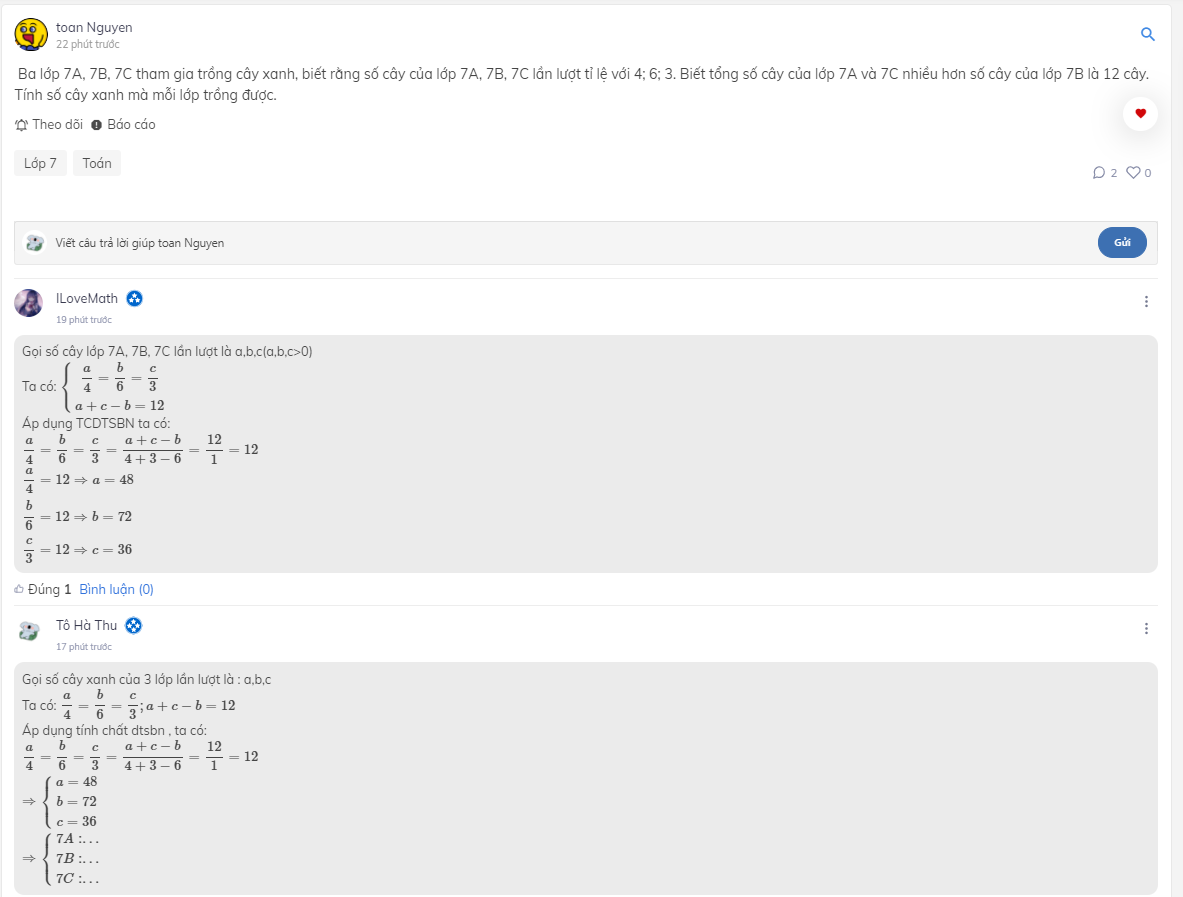
Gọi số cây trồng được của lớp 7A,7B,7C là a,b,c(cây)(a,b,c∈N*)
Áp dụng t/c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=12.4=48\\b=12.6=72\\c=12.3=36\end{matrix}\right.\)
Vậy....

Gọi số cây lớp 7A, 7B, 7C lần lượt là a,b,c(a,b,c>0)
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}\\a+c-b=12\end{matrix}\right.\)
Áp dụng TCDTSBN ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\dfrac{a}{4}=12\Rightarrow a=48\\ \dfrac{b}{6}=12\Rightarrow b=72\\ \dfrac{c}{3}=12\Rightarrow c=36\)
Gọi số cây xanh của 3 lớp lần lượt là : a,b,c
Ta có: \(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3};a+c-b=12\)
Áp dụng tính chất dtsbn , ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}7A:...\\7B:...\\7C:...\end{matrix}\right.\)

Gọi số cây lớp 7A,7B,7C ll là a,b,c(cây;a,b,c>0)
Áp dụng t.c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a-b+c}{4-6+3}=\dfrac{12}{1}=12\\ \Leftrightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
Vậy ..

Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a(cây), b(cây),c(cây)
(Điều kiện: \(a\in Z^+;b\in Z^+;c\in Z^+\))
Số cây của lớp 7A,7B,7C lần lượt tỉ lệ với 6;4;5 nên ta có:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}\)
Tổng số cây trồng được của 2 lớp 7A,7B nhiều hơn của lớp 7C là 50 cây nên ta có: a+b-c=50
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b-c}{6+4-5}=\dfrac{50}{5}=10\)
=>a=60;b=40;c=50
Vậy: Lớp 7A trồng được 60 cây
Lớp 7B trồng được 40 cây
Lớp 7C trồng được 50 cây

Gọi số cây mà `3` lớp trồng được lần lượt là `x,y,z (x,y,z \in \text {N*})`
Vì số cây của `3` lớp lần lượt tỉ lệ với `3:4:5`
Nghĩa là: `x/3=y/4=z/5`
Số cây trồng được của lớp `7A, 7B` nhiều hơn lớp `7C` là `40` cây
`-> x+y-z=40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/3=y/4=z/5=(x+y-z)/(3+4-5)=40/2=20`
`-> x/3=y/4=z/5=20`
`-> x=20*3=60, y=20*4=80, z=20*5=100`
Vậy, số cây của `3` lớp lần lượt là `60` cây, `80` cây, `100` cây.
Gọi số cây trồng được của 3 lớp 7A,7B,7C lần lượt là \(x,y,z\)(cây) \((x,y,z \in N*)\)
Do số cây trồng được của 3 lớp 7A,7B,7C lần lượt tỉ lệ với 3,4,5 nên:\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do số cây trồng được của 2 lớp 7A,7B nhiều hơn số cây trồng được của lớp 7C là 40 cây nên \(x+y-z=40\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y-z}{3+4-5}=\dfrac{40}{2}=20\)
Do đó:
\(\dfrac{x}{30}=20\Rightarrow x=60\)
\(\dfrac{y}{4}=20\Rightarrow y=80\) \(\left(TM\right)\)
\(\dfrac{z}{5}=20\Rightarrow z=100\)

\(\text{Gọi số cây lớp 7A; 7B; 7C trồng đc lần lượt là x; y; z}\)\(\text{Theo đề bài, ta có: }\)
\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{3}\)
\(\text{Áp dụng tính chất của hai dãy tỷ số bằng nhau, ta có:}\)
\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{3}=\dfrac{\left(x+z\right)-y}{\left(4+3\right)-6}=\dfrac{12}{1}=12\)
\(\left\{{}\begin{matrix}\dfrac{x}{4}=12;x=12.4=48\\\dfrac{y}{6}=12;y=12.6=72\\\dfrac{z}{3}=12;z=12.3=36\end{matrix}\right.\)
\(\text{Vậy số cây của 3 lớp 7A; 7B; 7C trồng đc lần lượt là 48; 72; 36}\)
\(\text{Nếu thấy hay thì cho xin cái li.ke nha bn ôi}\)

Gọi số cây 7A,7B,7C lần lượt là \(a,b,c(a,b,c\in \mathbb{N^*})\)
Áp dụng tc dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{c}{8}=\dfrac{a+b+c}{5+7+8}=\dfrac{120}{20}=6\\ \Rightarrow\left\{{}\begin{matrix}a=30\\b=42\\c=48\end{matrix}\right.\)
Vậy ...