Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(a,\left\{{}\begin{matrix}AB=AC\\BM=MC\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\\ b,\left\{{}\begin{matrix}BM=MC\\\widehat{AMB}=\widehat{CMD}\left(đđ\right)\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABC}=\widehat{BCD}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}CD\\ c,\left\{{}\begin{matrix}BM=MC\\\widehat{AMC}=\widehat{BMD}\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\\ \Rightarrow\widehat{ACB}=\widehat{CBD}\\ \text{Mà 2 góc này ở vị trí slt nên }AC\text{//}BD\)
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=CD và AB//CD
b: Ta có: ABDC là hình bình hành
nên BD//AC
c: Ta có: AB//CD
nên \(\widehat{ABC}=\widehat{DCB}\)
a: Xét ΔABM và ΔDCM có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC=BD
c: ABDC là hình bình hành
=>AB//DC
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Ta có: AB//CD
AB\(\perp\)AC
Do đó: CD\(\perp\)CA
Xét ΔABC vuông tại A và ΔCDA vuông tại C có
AB=CD
AC chung
Do đó: ΔABC=ΔCDA
c: Ta có: ΔABC=ΔCDA
=>BC=DA
Xét ΔMCA và ΔMBD có
MC=MB
\(\widehat{CMA}=\widehat{BMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMCA=ΔMBD
=>\(\widehat{MCA}=\widehat{MBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)CD
Do đó: DC\(\perp\)DB
=>ΔDBC vuông tại D
a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>BD//CA
c: Xét ΔABC và ΔDCB có
AB=DC
BC chung
AC=DB
=>ΔABC=ΔDCB
d: Xét tứ giác AEDF có
AE//DF
AE=DF
=>AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>E,M,F thẳng hàng
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: BA=DC; AC=DB
Xét ΔBAC và ΔCDB có
BA=CD
AC=DB
BC chung
Do đó: ΔBAC=ΔCDB
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó: AEDF là hình bình hành
Suy ra: AD và FE cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng
Youcho tam giác nhọn ABC, AB<AC. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD a) chứng minh tam giác AMB=tam giác DMC b) chứng minh AB=DC c)chứng minh AB song song với CD
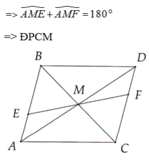
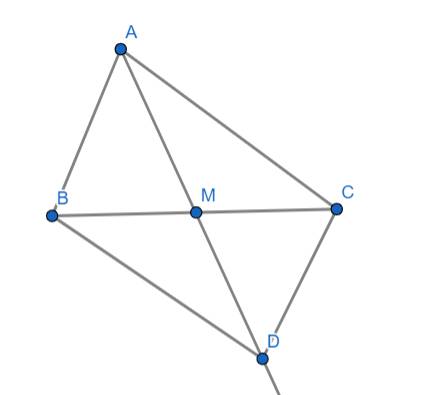
Hình vẽ:
=> \(AB=CD\) (2 cạnh tương ứng).
=> \(\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AB\) // \(CD.\)
b) Phải là \(BD\) // \(AC\) nhé.
Xét 2 \(\Delta\) \(AMC\) và \(DMB\) có:
\(AM=DM\left(gt\right)\)
\(\widehat{AMC}=\widehat{DMB}\) (vì 2 góc đối đỉnh)
\(MC=MB\) (vì M là trung điểm của \(BC\))
=> \(\Delta AMC=\Delta DMB\left(c-g-c\right)\)
=> \(\widehat{ACM}=\widehat{DBM}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AC\) // \(BD.\)
c) Vì \(\widehat{ABM}=\widehat{DCM}\left(cmt\right)\)
=> \(\widehat{ABC}=\widehat{DCB}.\)
Xét 2 \(\Delta\) \(ABC\) và \(DCB\) có:
Chúc bạn học tốt!