Cho một tam giác có AB=8cm AC =6cm BC=10,phân giác của góc BAC cắt đoạn BC tại D
a,Tính DB,DC ?
b,tính tỉ số diện tích của 2 tam giác ABD và ACD ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 3 2017
ta co: AB2+AC2=100 Ma BC2=100
\(\Rightarrow\Delta ABC\)vuong tai A
A, Trong \(\Delta ABC\)co AD la phan giac
\(\Rightarrow\frac{AB}{AC}=\frac{BD}{DC}\)(tinh chat duong phan giac)
\(\Rightarrow\frac{AB}{AB+AC}=\frac{BD}{BD+DC}\)\(\Rightarrow\frac{8}{8+6}=\frac{BD}{10}\Rightarrow BD=\frac{8.10}{14}=\frac{40}{7}cm\)
ta co: BD+DC=BC\(\Rightarrow DC=BC-BD=10-\frac{40}{7}=\frac{30}{7}cm\)
B, Ke duong cao AH
ta co: \(S_{\Delta ABD}=\frac{1}{2}AH.BD\)va \(S_{\Delta ACD}=\frac{1}{2}AH.DC\)
\(\Rightarrow\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}=\frac{40}{7}:\frac{30}{7}=\frac{4}{3}\)
Cho tam giác ABC có AB = 16cm, AC = 24cm, BC = 30cm. Đường phân giác của góc BAC cắt cạnh BC tại D.Qua D kẻ DE //AB (E AC) a/ Tính độ dài các đoạn thẳng DB, DC và DE. b/ Tính tỉ số diện tích của hai tam giác ABD và ACD.
AH
Akai Haruma
Giáo viên
1 tháng 5 2022
Lời giải:
a. $AB=AC=14$ cm nên $ABC$ là tam giác cân tại $A$
Do đó đường phân giác $AD$ đồng thời là đường trung tuyến
$\Rightarrow BD=DC=\frac{BC}{2}=6$ (cm)
b.
$\frac{S_{ABD}}{S_{ACD}}=\frac{BD}{CD}=1$
13 tháng 9 2023
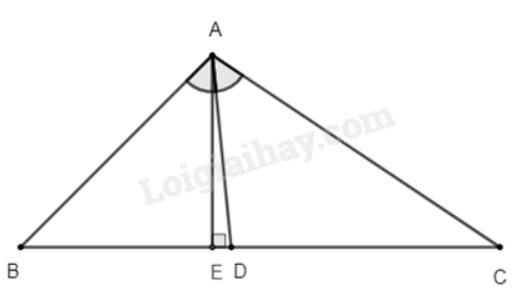
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).
21 tháng 2 2020
Xét t/gABC ta thấy AD là đường p/g của BAC
=>DB/DC=AB/AC (t/c phân giác)
Mà AB=15 cm ;AC=20cm nên ta có:
DB/DC=15/20
=> ta có tỉ lệ thức sau: DB/DB+DC=15/15+20 (t/c tỉ lệ thức)
=>DB/BC=15/35=>DB=15/35.BC=15/35.25=75/7(cm).
b) Ta kẻ AH _|_ BC
=>SABD=1/2AH.BD
=>SACD=1/2AH.DC
=>SABD/SACD=1/2AH.BD/1/2AH.DC=BD/DC
Mà ta thấy DB/DC=15/20=3/4
=> t/s SABD và SACD=3/4.
P/S: Bài này mik làm rồi nên hình mũi tên chỉ điển hình AB=15cm AC..... thôi nhé :< Cậu đừng ghi vào cũng được
19 tháng 4 2020
a) Xét tam giác BAD và CAD có:
AB=AC=14cm
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác)
AD cạnh chung
=> \(\Delta BAD=\Delta CAD\left(c.g.c\right)\)
=> BD=CD
Mà BD+CD=BC=12 cm
=> BD=DC=12:2=6(cm)
b) Vì AB=AC, BD=DC
=> AD là đường trung trực của BC
=> AD _|_ BC
=> \(S_{\Delta ABD}=\frac{1}{2}AD\cdot BD;S_{\Delta CAD}=\frac{1}{2}AD\cdot DC\)
\(\frac{S_{\Delta ABD}}{S_{\Delta CAD}}=\frac{AD\cdot BD}{AD\cdot DC}=\frac{AD}{DC}=1\)
21 tháng 2 2022
a: Xét ΔABC có AD là phân giác
nên BD/CD=AB/AC=3/4
BC=10cm
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{10}{7}\)
Do đó: BD=30/7(cm); CD=40/7(cm)
b: Xét ΔABC có DE//AC
nên DE/AC=BD/BC
=>DE/8=3/7
hay DE=24/7(cm)
31 tháng 3 2021
a) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DB}{DC}=\dfrac{6}{8}=\dfrac{3}{4}\)
a/Vì AD là tia ph/giác góc A nên \(\frac{AB}{AC}=\frac{DB}{DC}=\frac{8}{6}=\frac{4}{3}\Rightarrow DB=\frac{4}{3}DC\)
Vậy DB+DC=BC\(\Leftrightarrow\frac{4}{3}DC+DC=10\Leftrightarrow\frac{7}{3}DC=10\Leftrightarrow DC=\frac{30}{7}\)
suy ra DB=10-30/7=40/7
b/tam giác ABD và ACD chung đỉnh A và BD,DC cùng đ/thẳng nên cùng đ/cao \(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{BD}{DC}=\frac{4}{3}\)
giúp mk vs ạ mk đang cần gấp mk sẽ tick cho bn