tìm các nghiệm hữu tỉ của phương trình
\(a)7x^2+50x+7 \)
\(b)12x^2+7x-12=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 7 2019
2x^2 + x - 6
= 2x^2 + 4x - 3x - 6
= 2x(x + 2) - 3(x + 2)
= (2x - 3)(x + 2)
7x^2 + 50x + 7
= 7x^2 + x + 49x + 7
= 7x(x + 7) + x + 7
= (7x + 1)(x + 7)
12x^2 + 7x - 12
15x^2 + 7x - 2
= 15x^2 - 3x + 10x - 2
= 3x(5x - 1) + 2(5x - 1)
= (3x + 2)(5x - 1)
a^2 - 5a - 14
= a^2 + 2a - 7a - 14
= a(a + 2) - 7(a + 2)
= (a - 7)(a + 2)
2x^2 + 5x + 2
= 2x^2 + x + 4x + 2
= 2x(x + 2) + x + 2
= (2x + 1)(x + 2)
1 tháng 7 2019
\(2x^2+x-6=2x^2+4x-3x-6\)
\(=2x\left(x+2\right)-3\left(x+2\right)\)
\(=\left(x+2\right)\left(2x-3\right)\)
\(7x^2+50x+7\)
\(=7x^2+x+49x+7\)
\(=x\left(7x+1\right)+7\left(7x+1\right)\)
\(=\left(7x+1\right)\left(x+7\right)\)
\(12x^2+7x-12\)
\(=12x^2+16x-9x-12\)
\(=4x\left(3x+4\right)-3\left(3x+4\right)\)
\(=\left(3x+4\right)\left(4x-3\right)\)
SG
Dùng hệ thức Viet để tính nhẩm các nghiệm của phương trình:
a) x2 - 7x + 12 = 0; b) x2 + 7x+ 12 = 0.
2
QD
4 tháng 4 2017
a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = \(-\dfrac{-7}{1}\) = 7 = 3 + 4
x1x2 = \(\dfrac{12}{1}\) = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = \(\dfrac{-7}{1}\) = -7 = -3 + (-4)
x1x2 = \(\dfrac{12}{1}\) = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.
4 tháng 4 2017
a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = = 7 = 3 + 4
x1x2 = = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = = -7 = -3 + (-4)
x1x2 = = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.
18 tháng 6 2017
a) \(=7x^2+49x+x+7=7x\left(x+7\right)+\left(x+7\right)=\left(x+7\right)\left(7x+1\right)\)
c) \(=15x^2+10x-3x-2=5x\left(3x+2\right)-\left(3x+2\right)=\left(3x+2\right)\left(5x-1\right)\)
VN
18 tháng 6 2017
ta có : 7x2 + 49x + x + 7
= 7x(x + 7) + (x + 7)
= (x + 7) (7x + 1)
k mk mk k lại
CM
20 tháng 11 2017
a) x 2 – 7 x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 1 . 12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
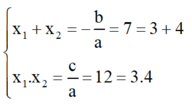
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
b) x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
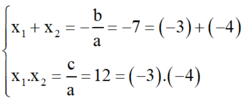
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.
B
2
KN
9 tháng 10 2020
Với \(y\ne\frac{7}{2}\)(Do y nguyên) thì\(y^2+2xy-7x-12=0\Leftrightarrow x\left(7-2y\right)=y^2-12\Leftrightarrow x=\frac{y^2-12}{7-2y}\)
Vì x nguyên nên \(\frac{y^2-12}{7-2y}\)nguyên \(\Rightarrow y^2-12⋮2y-7\Rightarrow4y^2-48⋮2y-7\Rightarrow\left(2y-7\right)^2+14\left(2y-7\right)+1⋮2y-7\Rightarrow1⋮2y-7\)\(\Rightarrow2y-7\inƯ\left(1\right)=\left\{\pm1\right\}\Rightarrow\orbr{\begin{cases}2y-7=-1\\2y-7=1\end{cases}}\Rightarrow\orbr{\begin{cases}y=3\\y=4\end{cases}}\)
* Với y = 3 thì x = -3
* Với y = 4 thì x = -4
Vậy phương trình có 2 cặp nghiệm nguyên (x; y) = (-3; 3) ; (-4; 4)
18 tháng 10 2020
Giúp mình bài này với nhé: tìm GTNN của thương của phép chia (4x^5+4x^4+4x^3-x-1):(2x^3+x-1), nhớ là đặt phép chia giùm mình luôn đừng ghi kết quả thôi nhé