Vật dao động điều hòa với tần số f= 0,5Hz. Tại t=0, vật có li độ x= 4cm và vận tốc v= +4π cm/s. Viết phương trình dao động của vật.
Giải kỹ phần tìm φ vì mình không biết cách tìm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=20\left(\dfrac{rad}{s}\right)\)
\(A^2=x^2+\dfrac{v^2}{\omega}\)
\(\Rightarrow A=\sqrt{\left(-4\right)^2+\dfrac{\left(-80\right)^2}{20^2}}=4\sqrt{2}\)
\(cos\varphi=\dfrac{4}{4\sqrt{2}}=\dfrac{1}{\sqrt{2}}\Rightarrow\varphi=\dfrac{\pi}{4}\)
Phương trình dao động:
\(x=4\sqrt{2}cos\left(20t+\dfrac{\pi}{4}\right)\)

Combo 3 câu :)
4/ \(f=5Hz\Rightarrow\omega=10\pi\left(rad/s\right)\)
\(A^2=x^2+\frac{v^2}{\omega^2}\Leftrightarrow A=\sqrt{\left(2\sqrt{3}\right)^2+\frac{20^2\pi^2}{10^2\pi^2}}=4\left(cm\right)\)
\(2\sqrt{3}=4\cos\varphi\Rightarrow\varphi=\pm\frac{\pi}{6}\)
\(v=-20\pi< 0\Rightarrow\varphi>0\Rightarrow\varphi=\frac{\pi}{6}\)
\(\Rightarrow x=4\cos\left(10\pi t+\frac{\pi}{6}\right)\)
5/ \(A^2=\frac{a^2}{\omega^4}+\frac{v^2}{\omega^2}\Rightarrow A=\sqrt{\frac{a^2}{\omega^4}+\frac{v^2}{\omega^2}}=...\)
6/ Áp dụng công thức ở câu 5

Đáp án B
Vật đi qua vị trí có li độ là x = -2 cm và đang hướng về phía vị trí biên gần nhất nên: v = -10 cm/s
Biên độ dao động của vật: A 2 = x 2 + v 2 ω 2 = ( - 2 ) 2 + ( - 10 ) 2 5 2 ⇒ A = 2 2 cm
Tại thời điểm ban đầu:
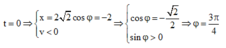
Phương trình dao động của vật là: x = 2 2 cos ( 5 t + 3 π 4 )

Đáp án B
Vật đi qua vị trí có li độ là x = − 2 cm và đang hướng về phía vị trí biên gần nhất nên: v = − 10 cm / s
Biên độ dao động của vật:
A 2 = x 2 + v 2 ω 2 = − 2 2 + − 10 2 5 2 = 8 ⇒ A = 2 2 cm
Tại thời điểm ban đầu:
t = 0 ⇒ x = 2 2 cosφ = − 2 v < 0 ⇒ cosφ = − 2 2 sinφ > 0 ⇒ φ = 3 π 4
Phương trình dao động của vật là: x = 2 2 cos 5 t + 3 π 4 cm

Đáp án C

Vận tốc cực đại của dao động a m a x = ω A = 4 π cm / s
Tại thời điểm t = 0,25 s vật có vận tốc v = 2 2 x m a x = 2 π 2 cm / s
Tại thời điểm t=0 ứng với góc lùi ∆ φ = ω ∆ t = 0 , 25 π
Biễu diễn các vị trí tương ứng trên đường tròn. Ta thu được φ 0 = - π 2 r a d
Phương trình dao động của vật là x = 4 cos ( πt - π 2 ) c m
giải
tần số góc \(\omega=2\pi f=2\pi.0,5=\pi\left(rad/s\right)\)
biên độ dao động
\(A=\sqrt{x^2+\frac{v^2}{\omega^2}}=\sqrt{4^2+\frac{4^2}{\pi^2}}\approx4,2cm\)
Pha ban đầu: Tại t = 0 vật có li độ x = 4cm và vận tốc v = 4cm/s (vật chuyển động theo chiều dương) nên pha ban đầu \(\varphi=-\frac{\pi}{4}rad\)
suy ra phương trình dao động
\(x=4,2.\cos\left(\pi t-\frac{\pi}{4}\right)cm\)
Tại sao φ bằng \(-\frac{\varphi}{4}\) ạ?