Tập hợp các giá trị a để\(\frac{2a+5}{a+1}\)là số nguyên dương và S = ........
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{2a+5}{a+1}=\frac{2\left(a+1\right)+3}{a+1}=2+\frac{3}{a+1}=>a+1=Ư\left(3\right)=\left\{-1;1;-3;3\right\}\)
=>a={-4;-2;0;2}

Để \(\frac{2a+5}{a+1}\)là số nguyên dương
=>2a+5 chia hết cho a+1
=>2a+2+3 chia hết cho a+1
=>2.(a+1)+3 chia hết cho a+1
=>3 chia hết cho a+1
=>a+1=Ư(3)=(1,3)
=>a={0,2}
Vậy S={0,2}

Đáp án A
Ta có 4 sin 2 x + 5 cos 2 x ≤ m . 7 cos 2 x ⇔ 4 1 - cos 2 x + 5 cos 2 x ≤ m . 7 cos 2 x ⇔ m ≥ 4 28 cos 2 x + 5 7 cos 2 x
Đặt t = cos 2 x , 0 ≤ t ≤ 1 khi đó m ≥ 4 28 t + 5 7 t = g t
Phương trình đã cho có nghiệm ⇔ m ≥ m i n 0 ; 1 g t
Dễ thấy g ' t < 0 ∀ t ∈ 0 ; 1 ⇒ m i n 0 ; 1 g t = g 1 = 6 7 ⇒ m ≥ 6 7 là giá trị cần tìm
Vậy a + b + c = 13.

Ta có :
\(\frac{2a+5}{a+1}\)là số nguyên dương => 2a + 5 chia hết cho a + 1
=> (2a + 2) + 3 chia hết cho a + 1
=> 2(a + 1) + 3 chia hết cho a + 1
=> 3 chia hết cho a + 1
=> \(a+1\in\left\{1;3\right\}\)
=> \(a\in0;2\)
\(\frac{2a+5}{a+1}=\frac{2\left(a+1\right)+3}{a+1}=2+\frac{3}{a+1}=>a+1=Ư\left(3\right)=\left\{-1;1;-3;3\right\}\)
=>a={-2;0;-4;2}
mà a là số tự nhiên=>a={0;2}

Ta có :
\(A=\frac{3x+5}{2+x}=\frac{3x+6-1}{2+x}=\frac{3.\left(x+2\right)-1}{2+x}=3-\frac{1}{2+x}\)
để S có giá trị nguyên thì \(\frac{1}{2+x}\in Z\)
\(\Rightarrow\)2 + x \(\in\)Ư ( 1 ) = { 1 ; -1 }
\(\Rightarrow\)x = -1 ; x = -3
khi đó : S = { -1 ; -3 }

Đáp án A
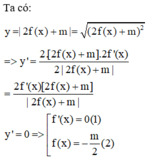
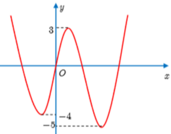
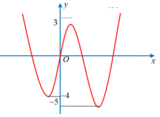
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
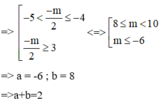

\(\frac{2a+5}{a+1}=\frac{2\left(a+1\right)+3}{a+1}=2+\frac{3}{a+1}\)
để 2a+5/a+1 là số nguyên thì 3/a+1 là số nguyên=>a+1 thuộc Ư(3)={-1;-3;1;3}
+)a+1=-1=>a=-2(loại)
+)a+1=-3=>a=-4(loại)
+)a+1=1=>a=0(nhận)
+)a+1=3=>a=2(nhận)
vậy...(bạn làm đúng rồi)
tick nhé