Một miếng bìa hình tam giác vuông, khi tăng mỗi cạnh góc vuông 2cm thì diện tích miếng bìa tăng 17cm². Khi giảm cạnh góc vuông này 3cm và cạnh góc vuông kia 1cm thì diện tích giảm 11cm². Tính độ dài 2 cạnh góc vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 8 2019
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là 1 2 xy (cm2)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là: 1 2 ⋅ ( x + 3 ) ( y + 3 ) (cm2)
Diện tích tăng thêm 36cm2 nên ta có phương trình:
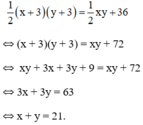
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là: 1 2 ( x − 2 ) ( y − 4 ) (cm2).
Diện tích giảm đi 26cm2 nên ta có phương trình
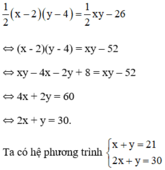
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được:
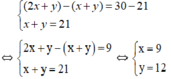
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
3 tháng 3 2021
một vật có khối lượng 124g và thể tích 15 cm3 là hợp kim của đồng và kẽm . tính xem trong đó có bao nhiêu gam đồng và bao nhiêu gam kẽm , biết rằng cứ 89 g đồng thì có thể tích là 10 cm3 và 7g kẽm có thể tích là 1 cm3
17 tháng 12 2019
1. Gọi độ dài ban đầu của các cạnh góc vuông lần lượt là: a; b ( a, b> 0; cm)
=> Diện tích của tam giác vuông ba đầu: \(\frac{1}{2}.a.b\)
Khi tăng mỗi cạnh 2 cm thì diện tích tăng 17 cm ^2
=> \(\frac{1}{2}\left(a+2\right)\left(b+2\right)=\frac{1}{2}.ab+17\)
<=> \(ab+2b+2a+4=ab+34\)
<=> \(a+b=15\)(1)
Khi giảm chiều dài cạnh kia 3cm và cạnh kia 1 cm thì diện tích giảm 11 cm^2
=> \(\frac{1}{2}\left(a-3\right)\left(b-1\right)=\frac{1}{2}ab-11\)
<=> \(ab-3b-a+3=ab-22\)
<=> \(-a-3b=-25\)(2)
Từ (1); (2) => a = 10; b = 5 ( thỏa mãn)
Vậy độ dài hai cạnh cần tìm là 10cm và 5 cm.
17 tháng 12 2019
Câu 2.
+) Gọi tuổi An hiện nay là x ( x>0; tuổi )
Khi đó tuổi cha An là: 3x (tuổi )
+) 5 năm trước
tuổi An là x - 5 ( tuổi )
tuổi cha An là : 3x - 5 ( tuổi )
Theo bài ra ta có phương trình :
3x - 5 = 4 ( x - 5)
<=> x = 15 ( tm)
Tuổi cha An là : 3 . 15 = 45 tuổi .
Cha An sinh An năm: 45 - 15 = 30 ( tuổi )
26 tháng 4 2016
1/ diện tích hình tam giác là 604,64 x 3/4 = 453,48 cm2
cạnh đáy tấm bìa là 453,48 x 2 : 24 =37,79cm
2/ độ dài cạnh góc vuông lớn là 62 x 3/5 = 37,2 cm
độ dài cạnh goc vuông bé là 62 - 37,2 = 24,8cm
diện tích tam giác là 37,2 x 24,8 : 2 =461,28 cm2
3/ độ dài cạnh góc vuông còn lại là 24 x 4/3 =32cm
chu vi ta giac là 32+24+40=96 cm
diện tích tam giác là 32 x 24 : 2 = 384cm2
26 tháng 4 2016
Mình biết câu 1 :
Diện tích hình tam giác là :
604,64 x 4/3 = 453,48 ( cm2 )
Cạnh đáy tấm bia hình tam giác là :
453,48 : 24 x 2 = 37,79
Đáp số : 37,79
các cậu bày mấy bài khac nha
4 tháng 4 2017
Bài giải:
Gọi x (cm), y (cm) là độ dài hai cạnh góc vuông của tam giác vuông. Điều kiện x > 0, y > 0.
Tăng mỗi cạnh lên 3 cm thì diện tích tăng them 36 cm2 nên ta được:
=
+ 36
Một cạnh giảm 2 cm, cạnh kia giảm 4 cm thì diện tích của tam giác giảm 36 cm2 nên ta được
=
- 26
Ta có hệ phương trình
Giải ra ta được nghiệm x = 9; y = 12.
Vậy độ dài hai cạnh góc vuông là 9 cm, 12 cm.
AH
Akai Haruma
Giáo viên
1 tháng 3 2022
Lời giải:
Gọi độ dài cạnh góc vuông ban đầu là $a,b$ (cm)
Theo bài ra ta có:
$(a+2)(b+3)=ab+50$
$\Leftrightarrow 3a+2b=44(1)$
Và:
$(a-2)(b-2)=ab-32$
$\Leftrightarrow -2a-2b+4=-32$
$\Leftrightarrow a+b=18(2)$
Từ $(1); (2)\Rightarrow a=8; b=10$ (cm)
7 tháng 3 2021
Gọi cạnh góc vuông lớn và cạnh góc vuông nhỏ lần lượt là a(cm) và b(cm)(Điều kiện: a>0; b>0; a>b)
Diện tích tam giác vuông là:
\(\dfrac{1}{2}ab\left(cm^2\right)\)
Vì khi tăng cạnh lớn lên 5cm và tăng cạnh nhỏ thêm 3cm thì diện tích tăng thêm 80cm2 nên ta có phương trình:
\(\dfrac{1}{2}\left(a+5\right)\left(b+3\right)=\dfrac{1}{2}ab+80\)
\(\Leftrightarrow\dfrac{1}{2}\left(ab+3a+5b+15\right)=\dfrac{1}{2}ab+80\)
\(\Leftrightarrow\dfrac{1}{2}ab+\dfrac{3}{2}a+\dfrac{5}{2}b+\dfrac{15}{2}=\dfrac{1}{2}ab+80\)
\(\Leftrightarrow\dfrac{3}{2}a+\dfrac{5}{2}b=\dfrac{145}{2}\)
\(\Leftrightarrow3a+5b=145\)(1)
Vì khi giảm mỗi cạnh đi 2cm thì diện tích giảm 35cm2 nên ta có phương trình:
\(\dfrac{1}{2}\left(a-2\right)\left(b-2\right)=\dfrac{1}{2}ab-35\)
\(\Leftrightarrow\dfrac{1}{2}\left(ab-2a-2b+4\right)=\dfrac{1}{2}ab-35\)
\(\Leftrightarrow\dfrac{1}{2}ab-a-b+2=\dfrac{1}{2}ab-35\)
\(\Leftrightarrow-a-b=-37\)
hay a+b=37(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}3a+5b=145\\a+b=37\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+5b=145\\3a+3b=111\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b=34\\a+b=37\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=17\\a=37-b=37-17=20\end{matrix}\right.\)(thỏa ĐK)
Vậy: Độ dài hai cạnh góc vuông lần lượt là 17cm và 20cm