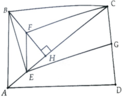
Cho hình chữ nhật ABCD vẽ BH vuông góc với AC tại H gọi E và F theo thứ tự là trung điểm của AB và CD Chứng minh rằng góc BEF
bằng 90 độ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) EF là đường trung bình của tam giác ABH => EF//AB; EF=1/2AB (1)
Có G là trung điểm của DC => GC//AB(DC//AB); GC=1/2AB(DC=AB) (2)
Từ (1)$(2) => EF//GC; EF=GC => Tứ giác EFCG là hình bình hành.
b) Xét tam giác EBH và tam giác CBH có:BH là cạnh chung
EHB=CHB=90 (gt)
EH=EC(H là trung điểm của EC)
Vậy tam giác EBH=tam giac CBH (cgv-cgv)
=>BEH=BCH ; EBH=CBH
Lại có:BEH+EBH+BCH+CBH=180 =>BEH=EBH=BCH=CBH=180/4=45 (3)
Co BCE+ECG=BCG
Ma BCG=90(ABCD là hcn); BCE=45(cmt)
=> ECG=45
Xét tam giác EGC có:EGC+GEC+ECG=180
=> EGC=180-(GEC+ECG)
=180-(90+45)=45 (4)
Tu (3)$(4) => BEG=90
c)Tu CM

Gọi N là trung điểm của BH
Xét ΔAHB có
E là trung điểm của AH(gt)
N là trung điểm của BH(theo cách gọi)
Do đó: EN là đường trung bình của ΔAHB(định nghĩa đường trung bình của tam giác)
⇒EN//AB và \(EN=\frac{AB}{2}\)(định lí 2 về đường trung bình của tam giác)
mà AB//CD và AB=CD(hai cạnh đối trong hình chữ nhật ABCD)
nên EN//CD và \(EN=\frac{CD}{2}\)
Ta có: EN//CD
mà F∈CD
nên EN//CF
Ta có: \(EN=\frac{CD}{2}\)(cmt)
mà \(CF=\frac{CD}{2}\)(do F là trung điểm của CD)
nên EN=CF
Xét tứ giác ENCF có EN//CF(cmt) và EN=CF(cmt)
nên ENCF là hình bình hành(dấu hiệu nhận biết hình bình hành)
⇒EF//NC(1)
Ta có: EN//AB(cmt)
AB⊥BC(\(\widehat{ABC}=90^0\))
Do đó: EN⊥BC
Gọi M là giao điểm của EN và BC
nên EN vuông góc với BC tại M
Xét ΔEBC có hai đường cao BH và EM cắt nhau tại N
nên CN⊥BE(2)
Từ (1) và (2) suy ra BE⊥EF
hay \(\widehat{BEF}=90^0\)

a: Xét ΔHAB có
M là trung điểm của HA
N là trung điểm của HB
Do đó: MN là đường trung bình
=>MN//AB và MN=AB/2
=>MN//KC và MN=KC
=>NCKM là hình bình hành
b; Xét ΔBMC có
BH là đường cao
MN là đường cao
BH cắt MN tại N
DO đó:N là trực tâm
=>CN vuông góc với BM
=>BM vuông góc với MK
hay góc BMK=90 độ

a, Chú ý EF là đường trung bình trong tam giác HAB
b, Chứng minh F là trực tâm tam giác BEC và sử dụng a)
c, Sử dụng tỉ số sinA trong tam giác vuông HAB và tỉ số tanA trong tam giác vuông BAC để tính AB, CB và AC, EC
Ta có BE//CF (AB//CD, \(E\in AB,F\in CD\) )
\(BE=CF\) (E là trung điểm của AB, F là trung điểm của CD, AB=CD)
\(\Rightarrow\) BECF là hình bình hành
Ta có: \(\widehat{BCF}=90^o\) (ABCD là hcn)
Do đó BECF là hình chữ nhật
\(\Rightarrow\widehat{BEF}=90^o\left(đpcm\right)\)
Còn yêu cầu nào nữa không bạn?