Cho ∆ABC vuông tại A có BC = 6cm , Góc b = 45° a) Tính AB , AC b) Diện tích ∆ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
0
TT
13 tháng 11 2020
a) Diện tích tam giác ABC (Heron)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(AB+BC+AC\right)\left(AB+BC-AC\right)\left(BC+AC-AB\right)\left(AC+AB-BC\right)}\)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(6+10+8\right)\left(6+10-8\right)\left(10+8-6\right)\left(8+6-10\right)}=24\left(cm^2\right)\)
b)Xét tam giác ABC có
\(BC^2=10^2=100\left(cm\right)\)
\(AB^2+AC^2=6^2+8^2=100\left(cm\right)\)
Vì 100cm=100cm
\(\Rightarrow BC^2=AB^2+AC^2\)
=> Tam giác ABC vuông tại A
Xét diện tích tam giác ABC thường \(S_{ABCt}=\frac{AH.BC}{2}\left(1\right)\)
Xét diện tích tam giác ABC vuông \(S_{ABCv}=\frac{AC.AB}{2}\left(2\right)\)
Từ (1) và (2)
\(\Leftrightarrow AH.BC=AB.AC\)
\(\Leftrightarrow AH.10=8.6\Leftrightarrow AH=4,8\left(cm\right)\)
Xét tam giác ABH vuông tại H
\(\Rightarrow BH^2=AB^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}\)
\(\Rightarrow BH=\sqrt{6^2-13,3^2}=3,6\left(cm\right)\)
Xét tam giác ACH vuông tại H
\(\Rightarrow HC^2=AC^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{8^2-4,8^2}=6,4\left(cm\right)\)
6 tháng 8 2021
a) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
8 tháng 2 2021
1) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
2) Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
3) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
30 tháng 4 2023
a: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm
c:
Xet ΔABC có
M là trung điểm của BC
MD//AC
=>D là trung điểm của AB
Xet ΔABC có
M là trung điểm của BC
ME//AB
=>E là trung điểm của AC
ΔAHC vuông tại H
mà HE là trung tuyến
nên HE=AE=CE=AC/2=4cm
ΔHAB vuông tại H
mà HD là trung tuyến
nên HD=AD=DB=AB/2=3cm
ED=AM=10/2=5cm
Vì HE^2+HD^2=ED^2
nên ΔHED vuông tại H
\(MH=\sqrt{5^2-4.8^2}=1,4\left(cm\right)\)
EM=AB/2=3cm
MH=1,4cm; EM=3cm; EH=4cm
\(P=\dfrac{1,4+3+4}{2}=4,2\left(cm\right)\)
\(S_{MHE}=\sqrt{4.2\cdot\left(4.2-1.4\right)\left(4.2-3\right)\left(4.2-4\right)}=1.68\left(cm^2\right)\)
\(S_{HED}=\dfrac{1}{2}\cdot4\cdot3=3\cdot2=6\left(cm^2\right)\)
=>\(S_{HMED}=6+1.68=7.68\left(cm^2\right)\)
AD
2 tháng 5 2023
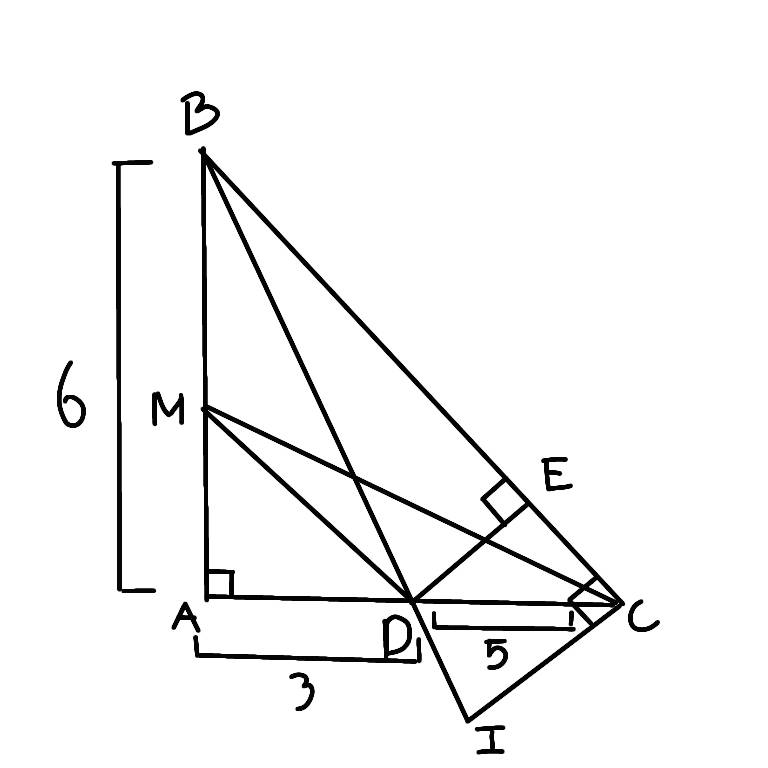a. Tính BC
BC^2 = AC^2 + AB^2
BC^2 = 6^2 + ( AD + DC )^2 = 8^2
BC^2 = 36 + 64 = 100
BC = căng bậc 100 = 10 cm
Tính tỉ số diện tích
Xét tam giác ABC có MD // BC
tam giác AMD ~ tam giác ABC
=>Diện tích tam giác AMD / Diện tích tam giác ABC = (AD/AC)^2=(3/8)^2=9/16 cm2
b.Xét tam giác AMD và tam giác EDC có
Góc MAD = góc CED = 90° (gt)
Góc D chung
=> tam giác AMD ~ tam giác EDC (g.g)
=>MD/AD = DC/EC
=>MD.EC=AD.DC
c. Xét tam giác BCI và tam giác BDE có
Góc BCI = Góc BED = 90°(gt)
Góc B chung
=> Tam giác BCI ~ tam giác BDE(g.g)
=> BC/BI = BD/BE
=> BC.BE = BI.BD(1)
Xét tam giác CBA và tam giác CDE có
Góc CAB = góc CED =90° (gt)
Góc C chung
=> Tam giác CBA ~ tam giác CDE(g.g)
=> CB/CA=CD/CE
=> CB.CE = CA.CD(2)
Từ (1) và (2) ta cộng cho 2 vế
=>BC.BE + CB.CE = BD.BI + CA.CD
=>(BE+CE)BC = BD.BI + CA.CD
=> BC.BC = BD.BI + CA.CD
=> BC^2 = BD.BI + CA.CD
MT
30 tháng 3 2022
a) Áp dụng định lý Pytagoo vào tam giác vuông ABC ta có:
BC2=AB2+AC2BC2=AB2+AC2
⇔⇔BC2=4,52+62=56,25BC2=4,52+62=56,25
⇔⇔BC=√56,25=7,5BC=56,25=7,5 cm
Xét ΔABCΔABCvà ΔDECΔDEC CÓ:
ˆBAC=ˆEDC=900BAC^=EDC^=900
ˆACBACB^ CHUNG
Suy ra: ΔABC ΔDECΔABC ΔDEC
⇒⇒BCEC=ACDCBCEC=ACDC ⇒⇒EC=BC.DCACEC=BC.DCAC
HAY EC=7,5×26=2,5EC=7,5×26=2,5
b) Áp dụng định lý Pytago vào tam giác vuông DEC ta có:
DE2=EC2−DC2DE2=EC2−DC2
⇔⇔DE2=2,52−22=2,25DE2=2,52−22=2,25
⇔⇔DE=√2,25=1,5DE=2,25=1,5
Vậy SDEC=DE.DC2=1,5×22=1,5SDEC=DE.DC2=1,5×22=1,5CM2
MT
30 tháng 3 2022
a) Áp dụng định lý Pytagoo vào tam giác vuông ABC ta có:
BC2=AB2+AC2BC2=AB2+AC2
⇔⇔BC2=4,52+62=56,25BC2=4,52+62=56,25
⇔⇔BC=√56,25=7,5BC=56,25=7,5 cm
Xét ΔABCΔABCvà ΔDECΔDEC CÓ:
ˆBAC=ˆEDC=900BAC^=EDC^=900
ˆACBACB^ CHUNG
Suy ra: ΔABC ΔDECΔABC ΔDEC
⇒⇒BCEC=ACDCBCEC=ACDC ⇒⇒EC=BC.DCACEC=BC.DCAC
HAY EC=7,5×26=2,5EC=7,5×26=2,5
b) Áp dụng định lý Pytago vào tam giác vuông DEC ta có:
DE2=EC2−DC2DE2=EC2−DC2
⇔⇔DE2=2,52−22=2,25DE2=2,52−22=2,25
⇔⇔DE=√2,25=1,5DE=2,25=1,5
Vậy SDEC=DE.DC2=1,5×22=1,5SDEC=DE.DC2=1,5×22=1,5CM2
a) Áp dụng tỉ số lượng giác:
\(sinB=\dfrac{AC}{BC}\Rightarrow AC=sin45^0.6=3\sqrt{2}\left(cm\right)\)
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=cos45^0.6=3\sqrt{2}\left(cm\right)\)
b) \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.3\sqrt{2}.3\sqrt{2}=9\left(cm^2\right)\)