Cho x2 + y2 - xy = 4. Tìm giá trị lớn nhất của biểu thức C = x2 + y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2+y^2+xy=3\)
Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)
\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\)
Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)
mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)
=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1
maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
Đặt \(P=x^2+y^2-xy\)
\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)
\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)
\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)
\(P_{min}=1\) khi \(x=y=1\)
\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow P\le9\)
\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)

Lời giải:
a. Áp dụng BĐT Cô-si:
$x^4+9\geq 6x^2$
$y^4+9\geq 6y^2$
$\Rightarrow x^4+y^4+18\geq 6(x^2+y^2)$
$A+18\geq 36$
$A\geq 18$
Vậy GTNN của $A$ là $18$ khi $x^2=y^2=3$
b.
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Leftrightarrow 12\geq (x+y)^2$
$\Rightarrow B=x+y\leq \sqrt{12}$. Vậy $B$ max bằng $\sqrt{12}$ khi $x=y=\sqrt{3}$
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 6\geq 2C$
$\Leftrightarrow C\leq 3$. Vậy $C_{\max}=3$. Giá trị này đạt tại $x=y=-\sqrt{3}$

Đáp án C
G T ⇔ x 2 + y − 3 x + y 2 − 4 y + 4 = 0 y 2 + x − 4 y + x 2 − 3 x + 4 = 0
có nghiệm ⇔ Δ x ≥ 0 Δ y ≥ 0 ⇔ 0 ≤ x ≤ 4 3 1 ≤ y ≤ 7 3
Và:
x y = 3 x + 4 y − x 2 − y 2 − 4 ⇒ P = 3 x 3 + 18 x 2 + 45 x − 8 ⏟ f x + − 3 y 3 + 3 y 2 + 8 y ⏟ g y
Xét hàm số f x = 3 x 3 + 18 x 2 + 45 x − 8 trên 0 ; 4 3 ⇒ max 0 ; 4 3 f x = f 4 3 = 820 9
Xét hàm số g x = − 3 y 3 + 3 y 2 + 8 y trên 1 ; 7 3 ⇒ max 1 ; 7 3 g x = f 4 3 = 80 9
Vật P ≤ max 0 ; 4 3 f x + max 1 ; 7 3 g x = 100
Dấu “=” xảy ra khi x = y = 4 3

Chọn B.
Phương pháp:
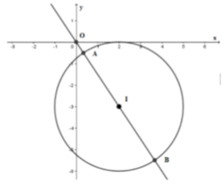
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
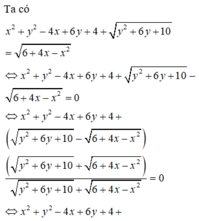
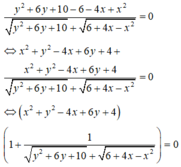


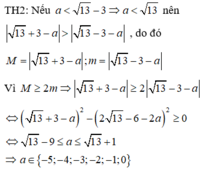

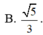
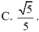
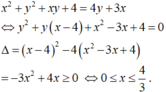
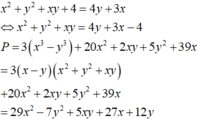
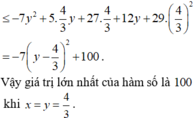


Xét \(x^2+y^2-xy=4\)
\(\Rightarrow x^2-2xy+y^2+xy=4\)
\(\Rightarrow\left(x-y\right)^2+xy=4\)
\(\Rightarrow xy=-\left(x-y\right)^2+4\)
Lại có: \(C=x^2+y^2=xy+4\)
\(=-\left(x-y\right)^2+4+4\)
\(=-\left(x-y\right)^2+8\)
Vì \(\left(x-y\right)^2\ge0\forall x,y\)
\(\Rightarrow-\left(x-y\right)^2\le0\forall x,y\)
\(\Rightarrow-\left(x-y\right)^2+8\le8\forall x,y\)
hay\(C\le8\forall x,y\)
GTLN là 8
Dấu "=" xảy ra khi: \(\left(x-y\right)^2=0\Rightarrow x=y\)
#DDN