Cho tam giác ABC , từ điểm D trên cạnh BC ta kẻ đường thẳng song song với các cạnh AB,AC chúng cắt các cạnh AC,AB theo thứ tự tại F và E. CMR : \(\frac{AE}{AB}+\frac{AF}{AC}=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

14 tháng 1 2018
Vì DF//AB (gt) . Áp dụng định lý Talet ta có : \(\frac{AF}{AC}=\frac{BD}{BC}\)(1)
Vì DE//AC (gt) . Áp dụng định lý Talet ta có : \(\frac{AE}{AB}=\frac{CD}{BC}\)(2)
Từ (1);(2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{BD}{BC}+\frac{CD}{BC}=\frac{BD+CD}{BC}=\frac{BC}{BC}=1\)(Đpcm)

CM
23 tháng 5 2019
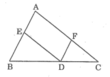
Trong tam giác ABC ta có: DE // AC (gt)
Suy ra: 
Lại có: DF // AB (gt)
Suy ra: 
Cộng từng vế (1) và (2) ta có:
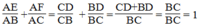
bạn tự vẽ hình nha
Xét \(\Delta ABC\) , vì \(DE\) // \(AC\left(gt\right)\) , ta có :
\(\frac{AE}{AB}=\frac{CD}{CB}\left(1\right)\)
Mà \(DF\) // \(AB\left(gt\right)\) , ta có :
\(\frac{AF}{AC}=\frac{BD}{BC}\left(2\right)\)
Ta cộng hai vế (1) và (2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{CB}+\frac{BD}{BC}=\frac{CD+BD}{BC}=\frac{BC}{BC}=1\)
Dài quá bạn ơi