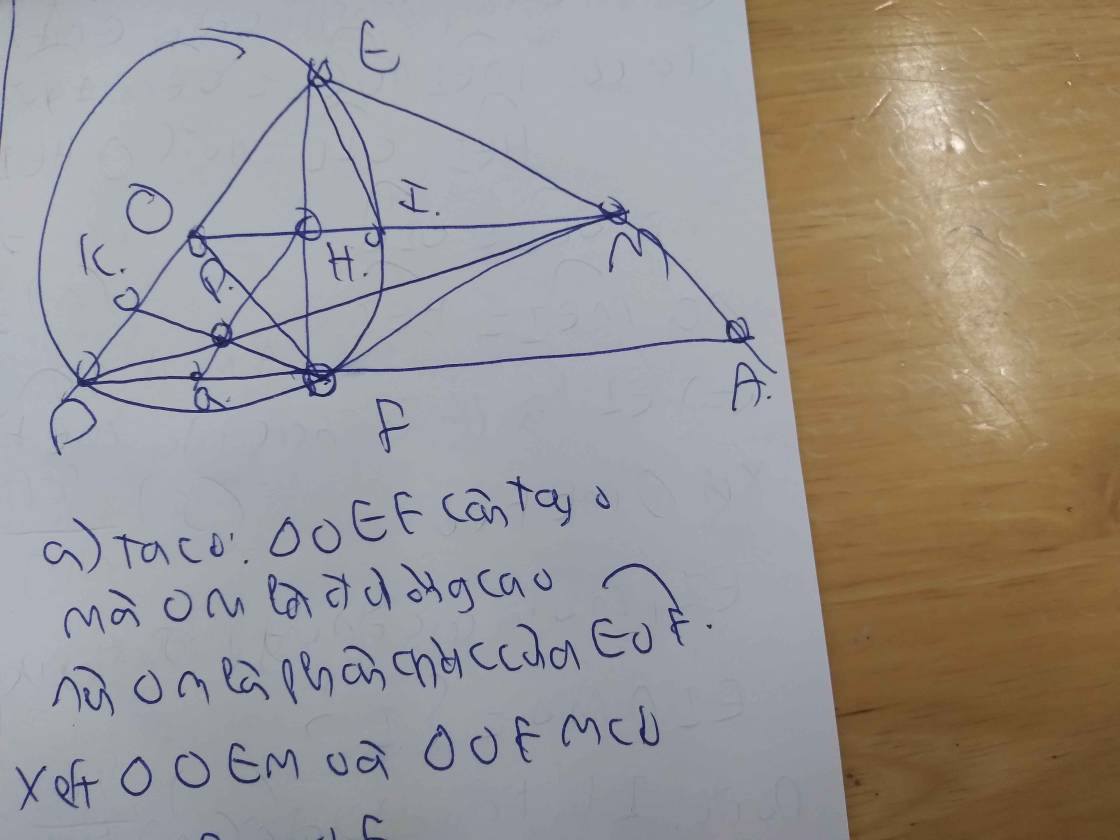
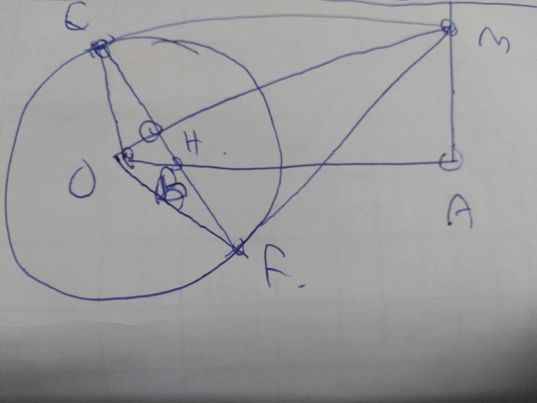
Cho đường tròn tâm O và điểm A ở ngoài đường tròn(O). Từ A kẻ đường thẳng (d) vuông góc với AO. M là một điểm trên d, từ M kẻ hai tiếp tuyến ME và MF đến (O) (E, F là hai tiếp điểm. MF cắt AE, AO thứ tự tại K và I.
a) Chứng minh năm điểm A, M, E, O, F cùng thuộc một đường tròn.
b) Chứng minh rằng MK.IF = MF.IK
c) Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định khi M di chuyển

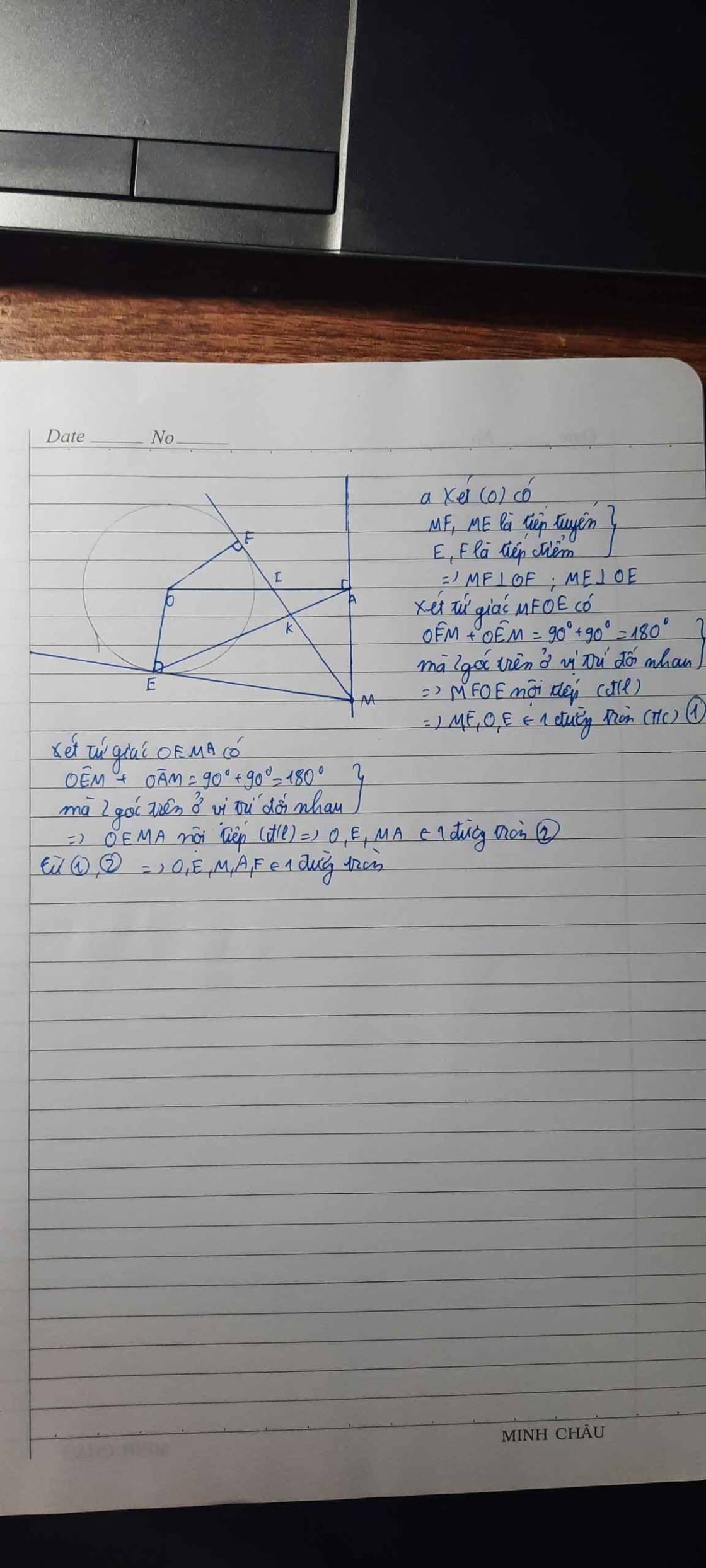







a, Xét tứ giác MEOF có \(\widehat{MEO}=\widehat{MFO}=90^0\)
=> Tứ giác MEOF nội tiếp (t/c)
=> 4 điểm M,E,O,F cùng thuộc đường tròn đường kính MO (1)
Xét tứ giác AFOM có : \(\widehat{MAO}=\widehat{MFO}=90^0\)
=> Tứ giác AFOM nội tiếp (t/c)
=> 4 điểm M,A,O,F cùng thuộc đường tròn đường kính MO (2)
Từ (1) và (2) => Năm điểm A, M, E, O, F cùng thuộc đường tròn đường kính MO