Cho AB=6cm. Một điểm C ở trong đoạn AB mà CA=3,6cm. Trên đường thẳng AB vẽ phía B. Hãy tìm một điểm D sao cho:
\(\frac{DA}{DB}\)=\(\frac{CA}{CB}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 2 2019
Ta có: CA=3,6cm =>CB=AB-CA=6-3,6=2,4cm
=> CA/CB=3,6/2,4=3/2
=> DA/DB=3/2
Mà ta có DA-DB=AB=6 cm ( Do điểm B nằm giữa A và D)
Áp dụng hiệu tỉ ta có:
DA=6:(3-2).3=18(cm)
2/\(\frac{AB}{CD}=\frac{2}{3}\Rightarrow\frac{AB}{2}=\frac{CD}{3}\Rightarrow\frac{AB}{4}=\frac{CD}{6}\)
\(\frac{CD}{EF}=\frac{4}{6}=\frac{2}{3}\Rightarrow\frac{CD}{2}=\frac{EF}{3}\Rightarrow\frac{CD}{6}=\frac{EF}{9}\)
=>\(\frac{AB}{4}=\frac{CD}{6}=\frac{EF}{9}=\frac{AB+CD+EF}{4+6+9}=\frac{70}{19}\)
=>AB=280/19 cm
CD=420/19 cm
EF=630/19 cm
Chúc e hc tốt :)
21 tháng 2 2020
Cô giáo của mk kết quả lại ra AB=16cm ,CD=24cm ,EF=30cm. mk ko hiểu là sai ở đâu ạ
12 tháng 5 2017
Giải
a) Từ giả thiết: \(\dfrac{AM}{MB}=\dfrac{7}{4}\Rightarrow\) \(\dfrac{\left(AM+MB\right)}{AM}=\dfrac{\left(7+4\right)}{7}=\dfrac{11}{7}\)
hay \(\dfrac{AB}{AM}=\dfrac{11}{7}:\dfrac{AM}{MB}=\dfrac{7}{4}\)
\(\Rightarrow\dfrac{AM+MB}{MB}=\dfrac{7+4}{4}=\dfrac{11}{4}\) hay \(\dfrac{AB}{BM}=\dfrac{11}{4}\)
b) Ta có: CB = AB - CA = 6cm - 3,6cm = 2,4cm
DA = AB + BD = 6 + BD
Từ giả thiết: \(\dfrac{DA}{DB}=\dfrac{CA}{CB}=\dfrac{3.6}{2.4}=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{\left(DB+6\right)}{DB}=\dfrac{3}{2}\)
\(\Rightarrow\) 2DB + 12 = 3DB \(\Rightarrow\) DB = 12 cm
CM
17 tháng 3 2019
Có hai trường hợp:
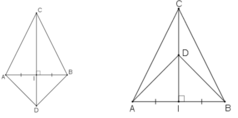
+ ΔAIC = ΔBIC (c.g.c) vì:
AI = IB (gt)
∠AIC = ∠BIC = 90o
CI chung.
+ ΔAID = ΔBID(c.g.c) vì:
AI = ID (gt)
∠AID = ∠BID = 90o
DI chung.
+ ΔACD = ΔBCD(c.c.c) vì:
AC = BC (Lấy từ ΔAIC = ΔBIC)
AD = BD (Lấy từ ΔAID = ΔBID)
CD chung
Ta có: \(CB=AB-AC=6-3,6=2,4cm\)
Và: \(DA=AB+BD=6+DB\)
Theo giả thiết: \(\frac{DA}{DB}=\frac{CA}{CB}=\frac{3,6}{2,4}=\frac{3}{2}\)
Thay: \(DA=6+DB\)
Ta có: \(\frac{6+DB}{DB}=\frac{3}{2}\Rightarrow2\left(6+DB\right)=3DB\Rightarrow12+2DB=3DB\Rightarrow DB=12cm\)
Phạm Thị Diệu Huyền
Cậu có áp dụng định lý Ta-let hok vậy?