cho hình chóp S.ABCD có đáy ABCD là hình thang cân (AB//CD) nội tiếp đường tròn tâm O và góc SBA=góc SCA=90 gọi M là trung điểm SA
a, CMR MO vuông góc (ABCD)
b, gọi \(\alpha\) là góc giữa 2 đường thẳng AB và SC. CMR \(\cos\alpha< \frac{BC}{SA}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 5 2019
Chọn C
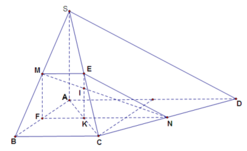
Ta gọi E, F lần lượt là trung điểm của SC, AB
Ta có ME//NF(do cùng song song với BC. Nên tứ giác MENF là hình thang, và 
hay tứ giác MENF là hình thang vuông tại M, F
Ta có: 
hay E là hình chiếu vuông góc của N lên (SAC)
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI
Suy ra, gọi
α
là góc giữa MN và (SAC) thì 
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Qua S kẻ đường thẳng d song song AD
Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)
Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)
\(AE=\dfrac{AB}{2}=a\)
\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(AC=\sqrt{AB^2+BC^2}=2a\) \(\Rightarrow AO=\dfrac{1}{2}AC=a\) ; \(AM=\dfrac{1}{2}AO=\dfrac{a}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCA}=45^0\)
\(\Rightarrow SA=AC.tan45^0=2a\)
\(AB^2=a^2\) ; \(AM.AC=\dfrac{a}{2}.2a=a^2\Rightarrow AB^2=AM.AC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AC}{AB}\Rightarrow\Delta ABM\sim\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{ABC}=90^0\Rightarrow BM\perp AC\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BM\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\left(SBM\right)\perp\left(SAC\right)\)
CM
2 tháng 5 2017
Đáp án A
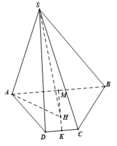
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) 
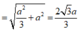
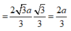
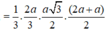
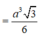
Từ giả thiết suy ra S nằm trên giao tuyến của 2 mặt phẳng qua B và C, lần lượt vuông góc AB và AC
Trong mặt phẳng (ABCD), qua B dựng d vuông góc AB, qua C dựng d' vuông góc AC, gọi H là giao điểm d và d' \(\Rightarrow H\) là hình chiếu vuông góc của S lên (ABCD)
Ta có các tam giác vuông ACH, ABH nội tiếp đường tròn đường kính AH nên ABCD nội tiếp đường tròn đường kính AH
\(\Rightarrow O\) là trung điểm AH \(\Rightarrow MO//SH\) (tính chất đường trung bình)
\(\Rightarrow MO\perp\left(ABCD\right)\)
Cũng từ trên ta suy ra M là tâm mặt cầu ngoại tiếp chóp S.ABCD
\(\Rightarrow SD\perp DA\)
Vì \(AB//CD\Rightarrow\alpha\) là góc giữa SC và CD
\(\Rightarrow cos\alpha=\left|cos\widehat{SCD}\right|=\sqrt{1-sin^2\widehat{SCD}}\)
Gọi K là hình chiếu vuông góc của M lên (SCD), do M là tâm mặt cầu ngoại tiếp \(\Rightarrow K\) là tâm đường tròn ngoại tiếp tam giác SCD
Áp dụng định lý hàm sin:
\(sin\widehat{SCD}=\frac{SD}{2ID}>\frac{SD}{2MD}=\frac{SD}{SA}\) (do M là tâm mặt cầu \(\Rightarrow MD=MA=\frac{1}{2}SA\))
\(\Rightarrow cos\alpha< \sqrt{1-\frac{SD^2}{SA^2}}=\sqrt{\frac{SA^2-SD^2}{SA^2}}=\frac{AD}{SA}=\frac{BC}{SA}\)