Cho Ot là tia phân giác của góc xOy ![]() (
(![]() xOy là góc nhọn). Lấy I bất kỳ thuộc Ot. Qua I kẻ IA vuông góc với Ox tại A và AI cắt Oy tại D. Qua I kẻ IB vuông góc với Oy tại B và IB cắt Ox tại C.
xOy là góc nhọn). Lấy I bất kỳ thuộc Ot. Qua I kẻ IA vuông góc với Ox tại A và AI cắt Oy tại D. Qua I kẻ IB vuông góc với Oy tại B và IB cắt Ox tại C.
a/ Chứng minh rằng : t.giác OIA =t.giác OIB
b/ Chứng minh rằng : t.giác OIC =t.giác OID và OC = OD
c/ OI![]() vuông góc với CD
vuông góc với CD

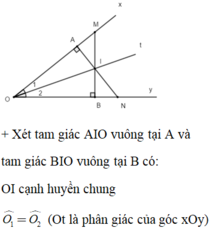

a) Xét \(\Delta\)OIA và \(\Delta\)OID có:
OAI = OBI (= 90o)
OI: chung
IOA = IOB (OI: phân giác AOB)
\(\Rightarrow\)\(\Delta\) OIA = \(\Delta\)OIB (ch-gn)
b) Xét \(\Delta\)OCB và \(\Delta\)ODA có:
OBC = OAD (= 90o)
OB = OA (\(\Delta\)OIA = \(\Delta\)OID)
COD: chung
\(\Rightarrow\Delta\) OCB = \(\Delta\)ODA (ch-gn)
\(\Rightarrow\)OC = OD (2 cạnh tương ứng)
Xét \(\Delta\)OIC và \(\Delta\)OID có:
OC = OD (cmt)
IOC = IOD (IO: phân giác COD)
IO: chung
\(\Rightarrow\Delta\) OIC = \(\Delta\)OID (c.g.c)
c) Gọi giao điểm của OI và CD là K
Xét \(\Delta\)OKC và \(\Delta\)OKD có:
OC = OD (cmt)
KOC = KOD (OI: phân giác COD)
OK: chung
\(\Rightarrow\Delta\) OKC = \(\Delta\)OKD (c.g.c)
\(\Rightarrow\)OKC = OKD (2 góc tương ứng)
Mà OKC + OKD = 180o
\(\Rightarrow\)OKC = OKD = 180o : 2
\(\Rightarrow\)OKC = OKD = 90o
\(\Rightarrow\)OI \(\perp\)CD