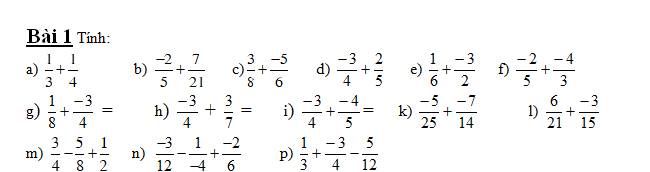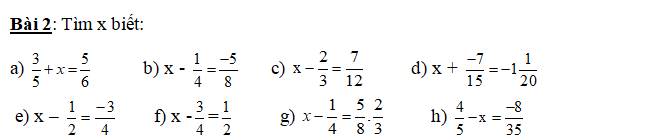Giúp mình vs ah gấp lắm ah
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em tham khảo:
Bác Hồ kính yêu được xem là bậc đại trí, đại nhân của dân tộc Việt Nam với những phẩm chất tuyệt vời từ trong con người Bác. Đã có bao tác phẩm thi ca nhạc họa ra đời để bày tỏ sự ngưỡng mộ, biết ơn và ca ngợi lối sống của vị cha gìa kính yêu của chúng ta. Và nét độc đáo nhất trong phong cách Hồ Chí Minh có lẽ chính là sự kết hợp hài hòa những phẩm chất tất khác nhau, thống nhất trong một con người. Đó là truyền thống và hiện đại, phương Đông và phương Tây, xưa và nay, dân tộc và quốc tế, vĩ đại và bình dị. Đó là sự kết hợp và thống nhất hài hòa bậc nhất trong lịch sử dân tộc Việt Nam từ xưa đến nay. Một mặt là tinh hoa con Lạc cháu hồng đúc nên Người, mặt khác tinh hoa nhân loại cũng góp phần làm nên phong cách Hồ Chí Minh. Bác tiếp thu chọn lọc, chắt chiu những tinh hoa của nhân loại để làm phong phú thêm lối sống của mình nhưng không Bao giờ Bác rời xa lối sống bình dị, phương đông - nơi Người đã sinh ra và lớn lên. Đó chính là một nét đẹp lớn, là sự tiếp thu biết chắt lọc vốn văn hóa nhân loại và đây cũng chính là bài học lớn cho mỗi người trên bước đường hội nhập với năm châu.

1: góc AHC+góc AKC=180 độ
=>AHCK nội tiếp
2: AHCK nội tiếp
=>góc AHK=góc ACK=1/2*sđ cung AC=góc ABC




Bài 1.
\(a,\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{4}{12}+\dfrac{3}{12}=\dfrac{7}{12}\)
\(b,\dfrac{-2}{5}+\dfrac{7}{21}=\dfrac{-42}{105}+\dfrac{35}{105}=\dfrac{-77}{105}=\dfrac{-11}{15}\)
\(c,\dfrac{3}{8}+\dfrac{-5}{6}=\dfrac{18}{48}+\dfrac{-40}{48}=\dfrac{-22}{48}=\dfrac{-11}{24}\)
\(d,\dfrac{-3}{4}+\dfrac{2}{5}=\dfrac{-15}{20}+\dfrac{8}{20}=\dfrac{-7}{20}\)
\(e,\dfrac{1}{6}+\dfrac{-3}{2}=\dfrac{2}{12}+\dfrac{-18}{12}=\dfrac{16}{12}=\dfrac{4}{3}\)
\(f,\dfrac{-2}{5}+\dfrac{-4}{3}=\dfrac{-6}{15}+\dfrac{-20}{15}=\dfrac{-26}{15}\)
\(g,\dfrac{1}{8}+\dfrac{-3}{4}=\dfrac{4}{32}+\dfrac{-24}{32}=\dfrac{20}{32}=\dfrac{5}{8}\)
\(h,\dfrac{-3}{4}+\dfrac{3}{7}=\dfrac{-21}{28}+\dfrac{12}{28}=\dfrac{-9}{28}\)
\(i,\dfrac{-3}{4}+\dfrac{-4}{5}=\dfrac{-15}{20}+\dfrac{-16}{20}=\dfrac{-31}{20}\)
\(k,\dfrac{-5}{25}+\dfrac{-7}{14}=\dfrac{-70}{350}+\dfrac{-175}{350}=\dfrac{-245}{350}=\dfrac{-7}{10}\)
\(l,\dfrac{6}{21}+\dfrac{-3}{15}=\dfrac{90}{315}+\dfrac{-63}{315}=\dfrac{27}{315}=\dfrac{3}{35}\)
\(m,\dfrac{3}{4}-\dfrac{5}{8}+\dfrac{1}{2}=\dfrac{24}{32}-\dfrac{20}{32}+\dfrac{1}{2}=\dfrac{4}{32}+\dfrac{1}{2}=\dfrac{1}{8}+\dfrac{1}{2}=\dfrac{2}{16}+\dfrac{8}{16}=\dfrac{10}{16}=\dfrac{5}{8}\)
\(n,\dfrac{-3}{12}-\dfrac{1}{-4}+\dfrac{-2}{6}=\dfrac{-1}{4}-\dfrac{1}{-4}+\dfrac{-1}{3}=0+\dfrac{-1}{3}=\dfrac{-1}{3}\)
\(p,\dfrac{1}{3}+\dfrac{-3}{4}-\dfrac{5}{12}=\dfrac{4}{12}+\dfrac{-9}{12}-\dfrac{5}{12}=\dfrac{-5}{12}-\dfrac{5}{12}=\dfrac{-10}{12}=\dfrac{-5}{6}\)
Bài 2:
\(a,\dfrac{3}{5}+x=\dfrac{5}{6}\)
\(x=\dfrac{5}{6}-\dfrac{3}{5}\)
\(x=\dfrac{7}{30}\)
\(b,x-\dfrac{1}{4}=\dfrac{-5}{8}\)
\(x=\dfrac{-5}{8}+\dfrac{1}{4}\)
\(x=\dfrac{-3}{8}\)
\(c,x-\dfrac{2}{3}=\dfrac{7}{12}\)
\(x=\dfrac{7}{12}+\dfrac{2}{3}\)
\(x=\dfrac{5}{4}\)
\(d,x+\dfrac{-7}{15}=-1\dfrac{1}{20}\)
\(x=-1\dfrac{1}{20}-\dfrac{-7}{15}\)
\(x=\dfrac{-7}{12}\)
\(e,x-\dfrac{1}{2}=\dfrac{-3}{4}\)
\(x=\dfrac{-3}{4}+\dfrac{1}{2}\)
\(x=\dfrac{-1}{4}\)
\(f,x-\dfrac{3}{4}=\dfrac{1}{2}\)
\(x=\dfrac{1}{2}+\dfrac{3}{4}\)
\(x=\dfrac{5}{4}\)
\(g,x-\dfrac{1}{4}=\dfrac{5}{8}\cdot\dfrac{2}{3}\)
\(x-\dfrac{1}{4}=\dfrac{5}{12}\)
\(x=\dfrac{5}{12}+\dfrac{1}{4}\)
\(x=\dfrac{2}{3}\)
\(h,\dfrac{4}{5}-x=\dfrac{-8}{35}\)
\(x=\dfrac{4}{5}-\dfrac{-8}{35}\)
\(x=\dfrac{36}{35}\)
#YVA


b:
Ta có: MN\(\perp\)AC
AB\(\perp\)AC
Do đó: MN//AB
Xét ΔACB có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
=>\(\dfrac{AN}{AC}=\dfrac{1}{2}\)
c:
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
=>MA=MB
=>ΔMAB cân tại M
Ta có: \(\widehat{DAB}+\widehat{MAB}=\widehat{MAD}=90^0\)
\(\widehat{HAB}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)
mà \(\widehat{MAB}=\widehat{HBA}\)(ΔMAB cân tại M)
nên \(\widehat{DAB}=\widehat{HAB}\)
=>AB là tia phân giác của góc DAH

It is believed that he won the prize in the contest yesterday.
He is believed to have won the prize in the contest yesterday.


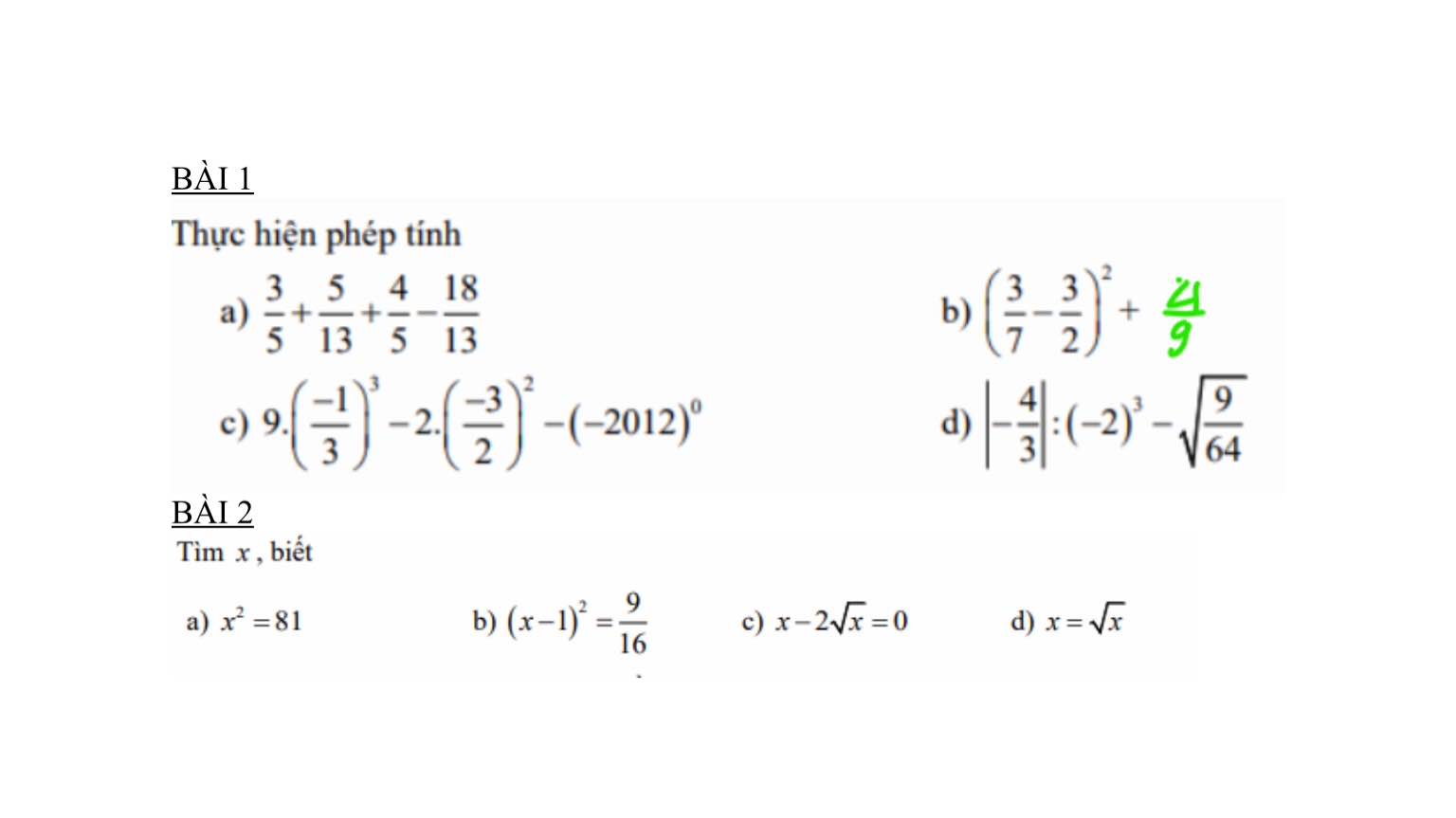 Mn lm giúp mình vs ah mình cần gấp !!!
Mn lm giúp mình vs ah mình cần gấp !!!