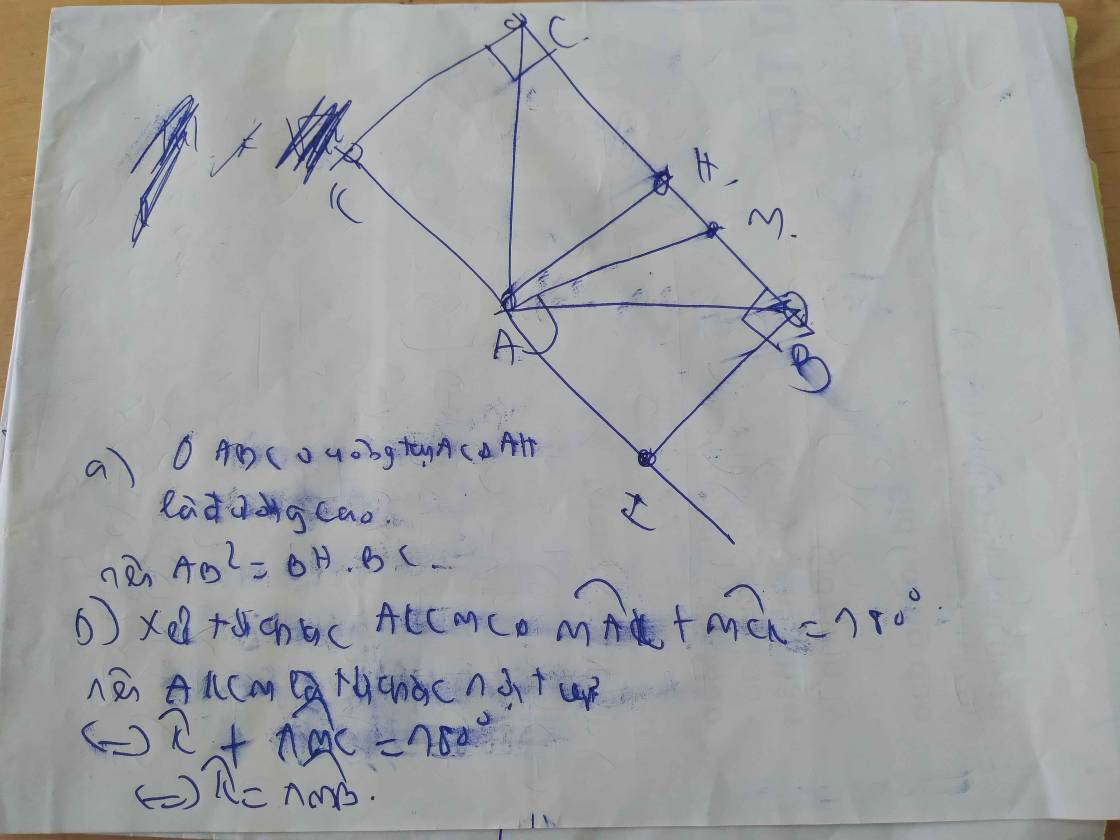
cho tam giác ABC vuông tại A , kẻ AH vuông góc với BC( H \(\in\)BC ) , trên đường thẳng vuông góc với BC tại C lấy điểm I sao cho CI=AH ( I và A thuộc 2 nửa mặt phẳng đối nhau bờ chứa cạnh BC ) . chứng minh rằng : HI=AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài làm
a) Xét tam giác AHC và tam giác ICH có:
AH = IC ( giả thiết )
\(\widehat{AHC}=\widehat{ICH}=90^0\)
HC chung
=> Tam giác AHC = tam giác ICH ( c.g.c )
=> HI = AC ( cạnh tương ứng )
b) ( Mik nghĩa là góc ABC = CIH thì hợp lí hơn )
Vì tam giác AHC = tam giác ICH ( cmt )
=> \(\widehat{CHI}=\widehat{HCA}\)
Ta có: \(\widehat{ABC}+\widehat{BCA}=90^0\)
hay \(\widehat{ABC}+\widehat{CHI}=90^0\)
Mà \(\widehat{CHI}+\widehat{CIH}=90^0\)
=> \(\widehat{ABC}=\widehat{CIH}\)
c) Một là hình mik bị sai, hai là đề bị lỗi nên k lm đc câu c.
Inosuke Hashibira, hình bn vẽ sai r.
Đề bài cho là I và A thuộc 2 nửa mặt phẳng đối nhau bờ chứa cạnh BC cơ mà!
Sao bn vẽ I và A cùng thuộc 1 nửa mp???!!!!!

Đáp án:
Giải thích các bước giải:
Hình bạn tự vẽ nhé!!
a). Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD là cạnh chung
Góc ABD = góc EBD (đường phân giác BD)
=> tam giác ABD=tam giác EBD (cạnh huyền-góc nhọn)
b). Gọi I là giao điểm của BD và AE.
Xét tam giác ABI và tam giác EBI có:
AB=EB (tam giác ABD=tam giác EBD)
Góc ABI=góc EBI (đường phân giác BD)
BI là cạnh chung.
=> tam giác ABI=tam giác EBI (c.g.c)
=> AI=EI => I là trung điểm của AE. (1)
=> Góc BIA=góc BIE
Mà góc BIA+góc BIE=180 độ (hai góc kề bù)
=> góc BIA=góc BIE=90 độ.
=> BI vuông góc với AE (2).
Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AE
d). Xét tam giác ADF vuông tại A và tam giác EDC vuông tại E có:
AD=ED (tam giác ABD = tam giác EBD)
AF=CE (GT)
=> tam giác ADF=tam giác EDC (hai cạnh góc vuông)
=> Góc ADF = góc EDC
cho xin tích ạ
Giải thích các bước giải:
Hình bạn tự vẽ nhé!!
a). Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD là cạnh chung
Góc ABD = góc EBD (đường phân giác BD)
=> tam giác ABD=tam giác EBD (cạnh huyền-góc nhọn)
b). Gọi I là giao điểm của BD và AE.
Xét tam giác ABI và tam giác EBI có:
AB=EB (tam giác ABD=tam giác EBD)
Góc ABI=góc EBI (đường phân giác BD)
BI là cạnh chung.
=> tam giác ABI=tam giác EBI (c.g.c)
=> AI=EI => I là trung điểm của AE. (1)
=> Góc BIA=góc BIE
Mà góc BIA+góc BIE=180 độ (hai góc kề bù)
=> góc BIA=góc BIE=90 độ.
=> BI vuông góc với AE (2).
Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AE
d). Xét tam giác ADF vuông tại A và tam giác EDC vuông tại E có:
AD=ED (tam giác ABD = tam giác EBD)
AF=CE (GT)
=> tam giác ADF=tam giác EDC (hai cạnh góc vuông)
=> Góc ADF = góc EDC