Xét các số thực x, y thỏa mãn
\(\sqrt{x^2+y^2+4x-2y+5}+\sqrt{x^2+y^2-8x-14y+65}=6\sqrt{2}\)
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức \(T=x^2+y^2-2x+2y+2\).Tính P = m + M
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo nhé!
Câu hỏi của Lê VĂn Chượng - Toán lớp 10 - Học toán với OnlineMath


Đáp án C
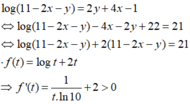
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

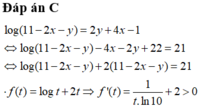
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Ta có: \(\sqrt{x^2+y^2+4x-2y+5}+\sqrt{x^2+y^2-8x-14y+65}=6\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(x+2\right)^2+\left(y-1\right)^2}+\sqrt{\left(4-x\right)^2+\left(7-y\right)^2}=6\sqrt{2}\left(^∗\right)\)
Xét hai vectơ \(\overrightarrow{u}=\left(x+2;y-1\right)\)và \(\overrightarrow{v}=\left(4-x;7-y\right)\)
Ta có: \(\overrightarrow{u}+\overrightarrow{v}=\left(6;6\right)\Rightarrow\left|\overrightarrow{u}+\overrightarrow{v}\right|=\sqrt{6^2+6^2}=6\sqrt{2}\)
Do vậy \(\left(^∗\right)\)trở thành\(\overrightarrow{u}+\overrightarrow{v}=\left|\overrightarrow{u}+\overrightarrow{v}\right|\)
Điều này xảy ra khi và chỉ khi \(\overrightarrow{u}\)và \(\overrightarrow{v}\)cùng hướng
\(\Leftrightarrow\hept{\begin{cases}\left(x+2\right)\left(7-y\right)=\left(y-1\right)\left(4-x\right)\\\left(x+2\right)\left(4-x\right)\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=x+3\\-2\le x\le4\end{cases}}\)
Khi y = x + 3 thì \(x^2+y^2-2x+2y+2=2x^2+6x+17\)
Xét hàm số \(f\left(x\right)=2x^2+6x+17\)trên đoạn \(\left[-2;4\right]\)
Ta có: \(-\frac{6}{2.2}=\frac{-3}{2}\in\left[-2;4\right]\)và \(f\left(-2\right)=13;f\left(-\frac{3}{2}\right)=\frac{25}{2};f\left(4\right)=73\)
Suy ra \(|^{min}_{\left[-2;4\right]}f\left(x\right)=\frac{25}{2}\);\(|^{max}_{\left[-2;4\right]}f\left(x\right)=73\)
Do đó \(m=\frac{25}{2};M=73\)và \(n+M=\frac{171}{2}\)
Vậy \(n+M=\frac{171}{2}\)