cho tam giác ABC. M là điểm trên cạnh BC. Gọi E,F lần lượt là hình chiếu của B và C trên đường thẳng AM. Chứng minh rằng BE+CF<BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ANME có
\(\widehat{ANM}=\widehat{AEM}=\widehat{EAN}=90^0\)
Do đó: ANME là hình chữ nhật
Suy ra: AM=NE

a: Xét ΔAMB và ΔKMC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)
MB=MC
Do đó: ΔAMB=ΔKMC
b: Xét tứ giác BECF có
BE//CF
BE=CF
Do đó: BECF là hình bình hành
Suy ra: BC và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của FE
hay F,M,E thẳng hàng

a) Kéo dài các tia AN; AE; AM; AF cho chúng cắt đường thẳng BC theo thứ tự tại các điểm G;H;I;K.
Xét \(\Delta\)ABI có: BM là phân giác ^ABI và BM vuông góc AI (tại M) => \(\Delta\)ABI cân tại B
=> BM đồng thời là đường trung tuyến \(\Delta\)ABI => M là trung điểm AI
C/m tương tự, ta có: N;E;F lần lượt là trung điểm của AG;AH;AK
Xét \(\Delta\)GAH: N là trung điểm AG; E là trung điểm AH => NE là đường trung bình \(\Delta\)GAH
=> NE // GH hay NE // BC (1)
Tương tự: MF // BC (2); NF // BC (3)
Từ (1); (2) và (3) => 4 điểm M;N;E;F thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).
b) Theo câu a ta có: NF là đường trung bình \(\Delta\)AGK => \(NF=\frac{GK}{2}=\frac{BG+BC+CK}{2}\)(*)
Lại có: \(\Delta\)ABG cân ở B; \(\Delta\)ACK cân ở C (câu a) nên BG = AB; CK = AC
Thế vào (*) thì được: \(NF=\frac{AB+BC+AC}{2}\),
KL: ...

Mình nói trước là mình mới học dạng này nên không chắc đâu nhé! Nhất là cái dấu "=" ấy, nó rất khó để giải thích và có thể sai. Nếu bạn dùng geogebra thì sẽ dễ hiểu hơn.
Đặt BC = a = const (hằng số)
Xét trường hợp E và F không trùng D. Khi đó theo quan hệ giữa đường vuông góc và đường xiên thì:
BE + CF < BD + CD = BC (1)
Nếu E và F trùng D thì BE + CF = BC (2)
Từ (1) và (2) suy ra \(BE+CF\le BC=const\)
Đẳng thức xảy ra khi E và F trùng D khi đó D là trung điểm BC và tam giác ABC cân tại A.
tth làm không đúng rồi.
Ta có E là hình chiếu của B lên AD
F là hình chiếu của CAD
=> \(BC=BD+DC\ge BE+CF\)
Dấu "=" xảy ra khi và chỉ khi \(E\equiv D\equiv F\)
khi đó: \(BD\perp AD;CD\perp AD\)=> D là chân đường cao hạ từ A đến BC
Vậy D là chân đường cao hạ từ A đến BC thì BE+CF đạt giá trị lớn nhất bằng BC

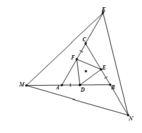
Theo giả thiết ta có: \(CF\perp AM\)nên \(\Delta MCF\)vuông tại F
Suy ra CF < MC (cạnh góc vuông bé hơn cạnh huyền) (1)
Tương tự ta có: BE < BM (2)
Từ (1) và (2) suy ra \(BE+CF< BM+MC=BC\)
Vậy \(BE+CF< BC\left(đpcm\right)\)
ta có:
tam giác BEM vuông tại E \(\Rightarrow\) BM là cạnh lớn nhất trong tam giác BEM
\(\Rightarrow\):BM>BE
ta có: tam giác MFC vuông tại F suy ra MC là cạnh lớn nhất trong tam giác FMC
\(\Rightarrow\) CM>CF
từ 2 điều trên \(\Leftrightarrow\)
BM+CM>CF+BE
BC>CF+BE