Cho một điểm m bất kì trong hình chữ nhật ABCD. Chứng minh:
MA2+MC2=MB2+MC2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
0
CM
25 tháng 5 2018
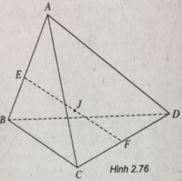
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
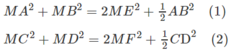
Cộng (1) và (2) ta có:
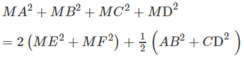
Gọi J là trung điểm của EF, ta có:
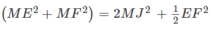
Khi đó:
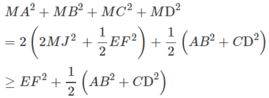
Vậy M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị nhỏ nhất khi M ≡ J.
PT
1
CM
5 tháng 7 2017
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.
CM
26 tháng 7 2017
Đáp án D
Ta có: M B 2 + M C 2 − M A 2 = M B → 2 + M C → 2 − M A → 2 = M I → + I B → 2 + M I → + I C → 2 − M I → + I A → 2
= M I 2 + 2 M I → I B → + I C → − I A → + I B 2 + I C 2 − I A 2
Gọi I là điểm thỏa mãn I B → + I C → − I A → = 0 → ⇒ I − 1 ; 2 ; 3
Suy ra M B 2 + M C 2 − M A 2 = M I 2 + I B 2 + I C 2 − I A 2 = 0 ⇔ M I = I A 2 − I B 2 − I C 2 = 2
Gọi K là giao điểm 2 đường chéo AC và BD => K là trung điểm AC và BD (tính chất HCN)
Trong tam giác MAC: MA^2 + MC^2 = 2*MK^2 + (1/2)*AC^2 (1) (công thức trung tuyến)
Trong tam giác MBD: MB^2 + MD^2 = 2MK^2 + (1/2)*BD^2 (2) (công thức trung tuyến)
Mặt khác AC = BD (đường chéo HCN) (3)
Từ (1), (2), (3) => MA^2 + MC^2 = MB^2 + MD^2 (đpcm)
thanks bạn nhiều