Giải phương trình:\((x^3+1)^3=16x-8\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2021
a, \(16x^2-\left(1+\sqrt{3}\right)^2=0\\ \Rightarrow\left(4x-1-\sqrt{3}\right)\left(4x+1+\sqrt{3}\right)=0\\ \Rightarrow\left[{}\begin{matrix}4x-1-\sqrt{3}=0\\4x+1+\sqrt{3}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt{3}}{4}\\x=\dfrac{-1-\sqrt{3}}{4}\end{matrix}\right.\)
b, \(x-2\sqrt{2x}+2=8\\ \Rightarrow x-\sqrt{8x}-6=0\\ \Rightarrow x-6=\sqrt{8x}\\ \Rightarrow\left(x-6\right)^2=\sqrt{8x}^2\\ \Rightarrow x^2-12x+36=8x\\ \Rightarrow x^2-20x+36=0\\ \Rightarrow\left(x^2-2x\right)-\left(18x-36\right)=0\)
\(\Rightarrow x\left(x-2\right)-18\left(x-2\right)=0\\ \Rightarrow\left(x-2\right)\left(x-18\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-18=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=18\end{matrix}\right.\)
22 tháng 8 2021
1: Ta có: \(16x^2-\left(\sqrt{3}+1\right)^2=0\)
\(\Leftrightarrow\left(4x-\sqrt{3}-1\right)\left(4x+\sqrt{3}+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}+1}{4}\\x=\dfrac{-\sqrt{3}-1}{4}\end{matrix}\right.\)
2: Ta có: \(x-2\sqrt{2x}+2=8\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)^2=8\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=2\sqrt{2}\\\sqrt{x}-2=-2\sqrt{2}\end{matrix}\right.\Leftrightarrow\sqrt{x}=2\sqrt{2}+2\)
\(\Leftrightarrow x=12+8\sqrt{2}\)
PT
1
CM
19 tháng 1 2017
Điều kiện : x ≠ 3 và x ≠ 1
Ta có: 16 x - 3 + 30 1 - x = 3 ⇔ 16(1 – x) +30(x -3) =3(x -3)(1 –x)
⇔ 16 – 16x +30x -90 =3x -3 x 2 -9 +9x
⇔ 3 x 2 +2x -65 =0
∆ ’ = 1 2 -3.(-65) = 1 + 195=196 > 0
∆ ' = 196 =14
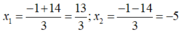
Giá trị của x thỏa mãn điều kiện bài toán
Vậy nghiệm của phương trình là x =13/3 và x =-5
4 tháng 4 2022
\(1,\dfrac{x-1}{3}=x+1\\ \Leftrightarrow x-1=3x+3\\ \Leftrightarrow3x-x=3+1\\ \Leftrightarrow x=2\)
PT có tập nghiệm S = {2}
\(2,\sqrt{16x^2+8x+1}-2=x\\ \Leftrightarrow\sqrt{\left(4x+1\right)^2}-2=x\\\Leftrightarrow 4x+1-2=x\\ \Leftrightarrow4x-x=2-1\\ \Leftrightarrow x=\dfrac{1}{3}\)
PT có tập nghiệm S = {1/3}
\(3,\left\{{}\begin{matrix}2x+y=17\\x-2y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=17\\2x-4y=2\end{matrix}\right.\\ \Leftrightarrow\left(2x+y\right)-\left(2x-4y\right)=17-2\\ \Leftrightarrow5y=15\\ \Leftrightarrow y=3\\ \Leftrightarrow2x+3=17\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\)
PTHH có tập nghiệm (x; y) là (7; 3)
LT
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2021
ĐKXĐ: \(x\ge-\dfrac{1}{2}\)
\(4x^3+4x^2-5x+9=4\sqrt[4]{\left(2x+1\right).2.2.2}\le2x+1+2+2+2\)
\(\Leftrightarrow4x^3+4x^2-7x+2\le0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-1\right)^2\le0\)
\(\Leftrightarrow\left(2x-1\right)^2\le0\) (do \(x+2>0\) ; \(\forall x\ge-\dfrac{1}{2}\))
\(\Rightarrow x=\dfrac{1}{2}\)
Vậy pt có nghiệm duy nhất \(x=\dfrac{1}{2}\)
HL
1
27 tháng 4 2020
\(\sqrt[3]{x+\frac{1}{2}}=16x^3-1\Leftrightarrow\sqrt[3]{x+\frac{1}{2}}-16x^3+1=0\Leftrightarrow x=0,5\)