Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HC, DC, EC
a) Diện tích tam giác DBE
b) Diện tích tứ giác EHIK
c) CMR: 3 × diện thích ABCD = 32 × diện tích EHIK.
Ai giải giúp mk câu c với ạ. Cảm ơn trc ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
24 tháng 12 2017
a)Ta có: DE=12DC(=12.12=6(cm)DE=12DC(=12.12=6(cm)
Nên SDBE=12.DE.BC=12.6.6,8=20,4(cm3)SDBE=12.DE.BC=12.6.6,8=20,4(cm3)
b)Ta có : HC=12BC=12.6,8=3,4(cm)HC=12BC=12.6,8=3,4(cm)
HI=12HC=12.3,4=1,7(cm)HI=12HC=12.3,4=1,7(cm)
EC = DE = 6cm
EK=KC=12EC=12.6=3(cm)EK=KC=12EC=12.6=3(cm)
Do đó SEHIK=SEHK+SHKI=12EK.HC+12HI.KCSEHIK=SEHK+SHKI=12EK.HC+12HI.KC
= 12EK.HC+12EK.HI=12EK(HC+HI)12EK.HC+12EK.HI=12EK(HC+HI)
SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)
Cách khác:
SEHIK=SEHC−SKIC=12EC.HC−12KC.ICSEHIK=SEHC−SKIC=12EC.HC−12KC.IC
= 12.6.3,4−12.3.1,712.6.3,4−12.3.1,7
= 10,2−2,55=7,65(cm2)
CM
12 tháng 12 2018
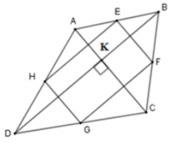
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)
Ngại làm quá nên chỉ lấy hình , vào TKHĐ là thấy :