1/Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I là trung điểm SD, E là điểm trên cạnh SB sao cho SE=3EB.
a, Tìm giao điểm K của CD với mặt phẳng (AIE)?
b) Tìm giao tuyến (d) của mp (AIE) với (SBC)
c) CM 3 đường thẳng (d), BC, AK đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2023
a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
\(A\in\left(ABCD\right)\cap\left(AIE\right)\)
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)
21 tháng 12 2023
a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)
8 tháng 12 2023
a: \(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
\(D\in FS\subset\left(SFE\right)\)
\(B\in SE\subset\left(SFE\right)\)
Do đó: \(BD\subset\left(SFE\right)\)
Ta có: \(O\in BD\subset\left(SEF\right)\)
\(O\in AC\subset\left(ACD\right)\)
Do đó: \(O\in\left(SEF\right)\cap\left(ACD\right)\)
mà \(D\in\left(SEF\right)\cap\left(ACD\right)\)
nên \(\left(SEF\right)\cap\left(ACD\right)=DO\)
b: Xét ΔSDB có
E,F lần lượt là trung điểm của SB,SD
=>EF là đường trung bình của ΔSDB
=>EF//DB
Xét (ABCD) và (AEF) có
BD//EF
\(A\in\left(ABCD\right)\cap\left(AEF\right)\)
Do đó: (ABCD) giao (AEF)=xy, xy đi qua A và xy//BD//EF
CM
27 tháng 5 2019
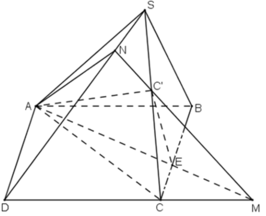
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE
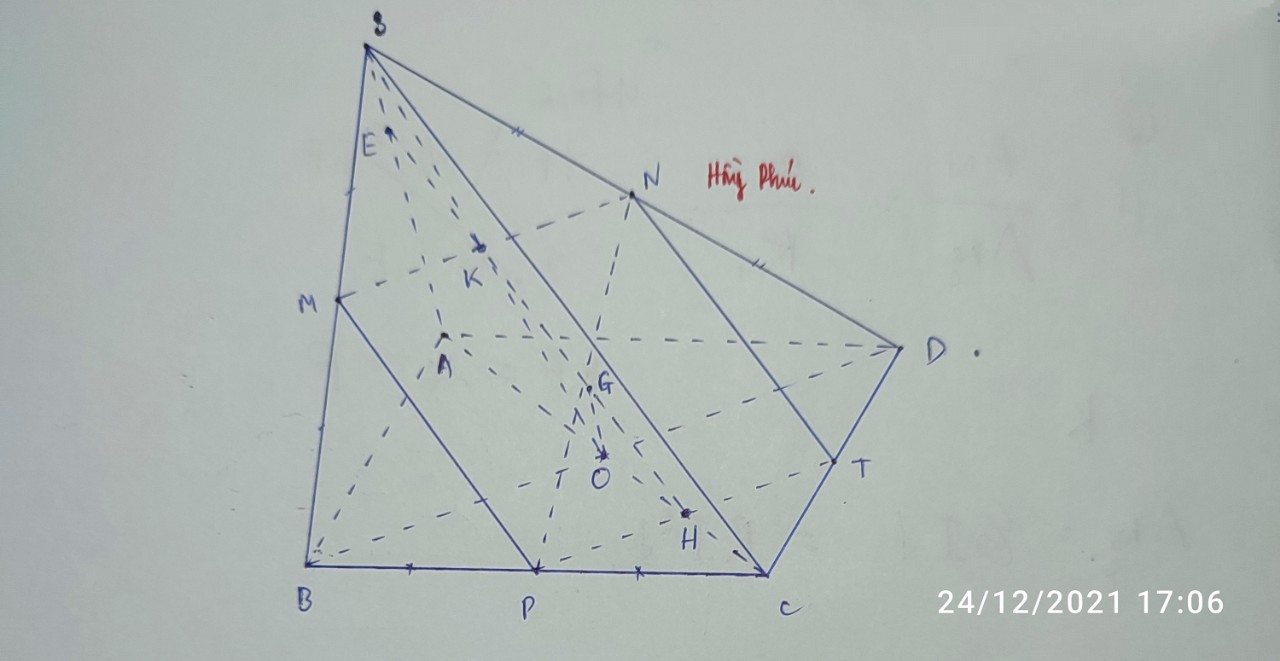
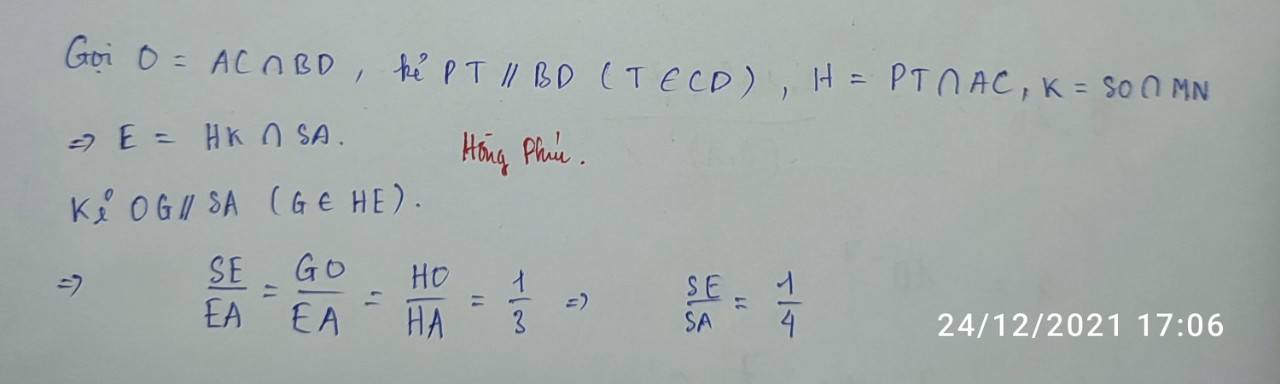
a Xem lại đề => Không làm được ý c
a, Gọi :
\(DB\cap AC=\left\{G\right\}\)
\(IE\cap SG=\left\{J\right\}\)
\(AJ\cap SC=\left\{H\right\}\)
\(\rightarrow\left(AIE\right)\cap\left(SBC\right)=HE\)
a. Xem lại đề > không làm được c
b. Gọi \(DB\cap AC=G\)
\(IE\cap SG=J\)
\(AJ\cap SC=H\)
\(\rightarrow\left(AIE\right)=\left(SBC\right)=HE\)