Cho biểu thức : \(M=\frac{1}{y-1}-\frac{y}{y+1}+\frac{2y^2}{y^2-1}\)
a) Với điều kiện nào của y thì giá trị của biểu thức M xác định
b) Rút gọn biểu thức M
c) Tìm điều kiện của y để M nhận được giá trị nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)
=>\(2m\ne4\)
=>\(m\ne2\)
b: Thay m=0 vào (d1), ta được:
\(y=\left(0-1\right)x+2=-x+2\)
Thay m=0 vào (d2), ta được:
\(y=\left(3-0\right)x-2=3x-2\)
Vẽ đồ thị:
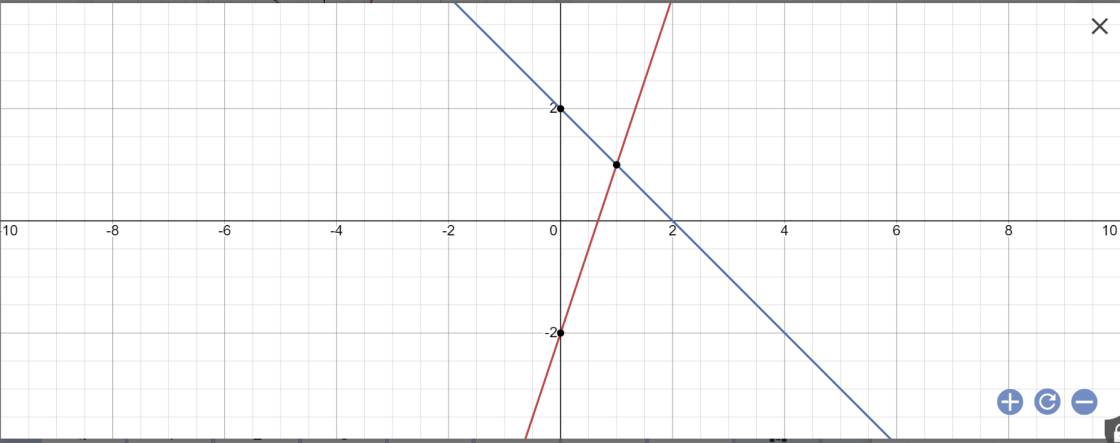
c: Phương trình hoành độ giao điểm là:
3x-2=-x+2
=>3x+x=2+2
=>4x=4
=>x=1
Thay x=1 vào y=3x-2, ta được:
y=3*1-2=3-2=1
d:
Khi m=0 thì (d2): y=3x-2
Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox
y=3x-2 nên a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq72^0\)
Câu 3:
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Ta có: AC//OM
OM\(\perp\)AB
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)CM tại E
Xét ΔMBC vuông tại B có BE là đường cao
nên \(ME\cdot MC=MB^2\)(3)
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)

\(M=\frac{4x+8}{x^2-1}:\frac{x+2}{x+1}-\frac{x-2}{1-x}\) \(ĐKXĐ:x\ne\pm1\)
\(M=\frac{4\left(x+2\right)}{\left(x-1\right)\left(x+1\right)}.\frac{x+1}{x+2}+\frac{x-2}{x-1}\)
\(M=\frac{4}{x-1}+\frac{x-2}{x-1}\)
\(M=\frac{4+x-2}{x-1}\)
\(M=\frac{x+2}{x-1}\)
vậy \(M=\frac{x+2}{x-1}\)

\(a,ĐK:9x^2-1\ne0\Leftrightarrow x^2\ne\frac{1}{9}\Leftrightarrow x\ne\pm\frac{1}{3}\)
\(b,M=\frac{\sqrt{9x^2-6x+1}}{9x^2-1}=\frac{\sqrt{\left(3x-1\right)^2}}{\left(3x-1\right)\left(3x+1\right)}=\frac{\left|3x-1\right|}{\left(3x-1\right)\left(3x+1\right)}\)
với \(3x-1>0\) ta có \(M=\frac{3x-1}{\left(3x-1\right)\left(3x+1\right)}=\frac{1}{3x+1}\)
với \(3x-1< 0\) ta có \(M=\frac{-\left(3x-1\right)}{\left(3x-1\right)\left(3x+1\right)}=-\frac{1}{3x+1}\)
\(c,\) th1 : \(M=\frac{1}{3x+1}\) khi \(x>\frac{1}{3}\) mà \(M=\frac{1}{4}\)
\(\Leftrightarrow\frac{1}{3x+1}=\frac{1}{4}\Leftrightarrow x=1\left(thoaman\right)\)
th2 : \(M=-\frac{1}{3x+1}\) khi \(x< \frac{1}{3}\) mà \(M=\frac{1}{4}\)
\(\Leftrightarrow\frac{-1}{3x+1}=\frac{1}{4}\Leftrightarrow3x+1=-4\Leftrightarrow x=-\frac{5}{3}\left(thoaman\right)\)
\(d,M=\frac{\left|3x-1\right|}{\left(3x-1\right)\left(3x+1\right)}< 0\) có \(\left|3x-1\right|>0\)
\(\Rightarrow\left(3x-1\right)\left(3x+1\right)< 0\)
th1 : \(\hept{\begin{cases}3x-1>0\\3x+1< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>\frac{1}{3}\\x< -\frac{1}{3}\end{cases}\left(voli\right)}}\)
th2 : \(\hept{\begin{cases}3x-1< 0\\3x+1>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< \frac{1}{3}\\x>-\frac{1}{3}\end{cases}\Leftrightarrow-\frac{1}{3}< x< \frac{1}{3}}\)

a) \(A=\frac{1}{y-1}-\frac{y}{1-y^2}\left(y\ne\pm1\right)\)
\(\Leftrightarrow A=\frac{1}{y-1}+\frac{y}{\left(y-1\right)\left(y+1\right)}=\frac{y+1}{\left(y-1\right)\left(y+1\right)}+\frac{y}{\left(y-1\right)\left(y+1\right)}=\frac{2y+1}{\left(y-1\right)\left(y+1\right)}\)
Thay y=2 (tm) vao A ta co:
\(A=\frac{2\cdot2+1}{\left(2-1\right)\left(2+1\right)}=\frac{5}{3}\)
Vay \(A=\frac{5}{3}\)voi y=2
b) Ta co: \(\hept{\begin{cases}A=\frac{2y+1}{\left(y-1\right)\left(y+1\right)}\left(y\ne\pm1\right)\\B=\frac{y^2-y}{2y+1}=\frac{y\left(y-1\right)}{2y+1}\left(y\ne\frac{-1}{2}\right)\end{cases}}\)
\(\Rightarrow M=\frac{2y+1}{\left(y-1\right)\left(y+1\right)}\cdot\frac{y\left(y-1\right)}{2y+1}=\frac{\left(2y+1\right)\cdot y\cdot\left(y-1\right)}{\left(y-1\right)\left(y+1\right)\left(2y+1\right)}=\frac{y}{y+1}\)
để M xác định
\(\Rightarrow\orbr{\begin{cases}y-1\ne0\\y+1\ne0\end{cases}}\Rightarrow\frac{y\ne1}{y\ne-1}.\)
\(b,M=\frac{1}{y-1}+\frac{y}{y+1}+\frac{2y^2}{y^2-1}\)
\(M=\frac{y+1}{\left(y+1\right)\left(y-1\right)}+\frac{y\left(y-1\right)}{\left(y-1\right)\left(y+1\right)}+\frac{2y^2}{\left(y+1\right)\left(y-1\right)}\)
\(M=\frac{y+1-y^2+y+2y^2}{\left(y+1\right)\left(y-1\right)}=\frac{1+2y+y^2}{\left(y+1\right)\left(y-1\right)}=\frac{\left(1+y\right)^2}{\left(y+1\right)\left(y-1\right)}\)
\(M=\frac{y+1}{y-1}\)
c, Để M nhận giá trị nguyên
\(\Rightarrow y+1⋮y-1\)
\(\Leftrightarrow y-1+2⋮y-1\)
\(\Rightarrow y-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
y = .... Tự tính