Cho tam giác ABV vuông tại A (AB<AC) trung tuyến AM đường cao AH . Trên tia đối của tia MA lấy điểm D sao cho MD=MA
a,Tứ giác ABDC là hình gì ?Vì sao?
b,Gọi I là điểm đối xứng của A qua BC .C/m BC//ID
c,C/m tứ giác BIDC là hình thang cân
d,Kẻ HE vuông góc với AB tại E,HE vuông góc AC tại F.C/m AM vuông góc với EF
Thanks

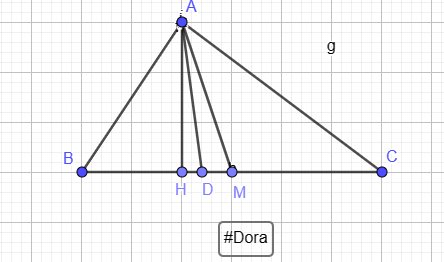
a) Xét tứ giác ABDC có 2 đường chéo AD và BC cắt nhau tại M là trung điểm mỗi đường
\(\rightarrow ABCD\) là hình bình hành
Lại có góc A vuông
\(\rightarrow ABCD\) là hình chữ nhật
b)
Ta có H và M là trung điểm của AI và AD
\(\rightarrow\)HM là đường trung bình của tam giác AID
\(\rightarrow HM//DI\)
\(\rightarrow BC//DI\)
c)
Xét tứ giác BIDC có \(BC//DI\)
\(\rightarrow\)\(BIDC\) là hình thang
d) Gọi I là giao của \(AM\) và \(EF\)
Ta chứng minh được \(\Delta ABC\) ~\(\Delta AFE\)
\(\rightarrow\widehat{AEI}=\widehat{AFE}=\widehat{ACB}\)
Do \(AM\) là tiếp tuyến của tam giác \(ABC\) vuông tại A
\(\rightarrow AM=MB=MC\)
\(\rightarrow\Delta AMB\) cân tại M
\(\widehat{EAI}=\widehat{BAM}=\widehat{ABM}=\widehat{ABC}\)
\(\rightarrow\widehat{AEI}+\widehat{EAI}=\widehat{ACB}+\widehat{ABC}\)
\(\rightarrow180^O-\left(\widehat{AEI}+\widehat{EAI}\right)=180^O-\left(\widehat{ACB}-\widehat{ABC}\right)\)
\(\rightarrow\widehat{EIA}=\widehat{BAC}=90^O\)
\(\rightarrow AM\perp EF\)