Cho tam giác ABC, D chia trong đoạn thẳng BC theo tỉ số 1:2; O chia trong đoạn AD theo tỉ số 3:2, K là giao điểm của BO và AC. Tính tỉ số AK:KC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
7 tháng 2 2022
hình tự vẽ hén:>
kẻ AL//BC
có: \(\dfrac{AL}{BC}=\dfrac{AM}{MC}\) ( hệ quả đl ta-lét)
theo giả thiết AM=\(\dfrac{1}{2}AC\) \(\Rightarrow\dfrac{AC}{AM}=2\)
\(\Rightarrow\dfrac{AC-AM}{AM}=\dfrac{2-1}{1}=1\Rightarrow\dfrac{MC}{AM}=1\)
\(\Leftrightarrow\dfrac{AL}{BC}=1\)
mặt khác ta có : \(\dfrac{BK}{BC}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{AL}{BC}.\dfrac{BC}{BK}=1.3=3\Rightarrow\dfrac{AL}{BK}=3\)
\(\Rightarrow\dfrac{BM}{BK}=\dfrac{1}{1}=1\)
15 tháng 11 2015
Gọi BD là phân giác của HAC
=>tam giác ABD cân tại A( có AD dồng thời là dg cao và pgiac)
=> BH=DH = 3a => DC =5a vì BH:HC =3:8
+ Áp dụng tính chất đường phân giác trong tam giác HAC
ta có : AC/AH =DC/DH
=> AC/6 =5/3 => AC =10
+ Áp dụng pita go cho HAC => HC = 8 => a =1
=>BC = 11a =11
=>S =AH.BC/2 =6.11/2 =33
CM
3 tháng 3 2019
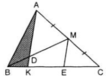
Kẻ ME song song với AK (E ∈ BC).
Ta có: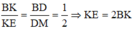 
ME là đường trung bình của tam giác ACK nên EC = KE = 2BK.
Ta có: BC = BK + KE + EC = 5BK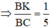 
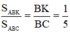(hai tam giác ABK và ABC có chung đường cao hạ từ A)