△ABC là tam giác gì biết: sinC=cosA+cosB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Ta có:
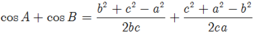
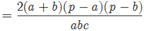
Vậy sin C = cosA + cos B khi và chỉ khi
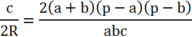
Hay ![]()
Nên c2[(a + b) 2 - c2]= (a + b)2[ c2 - (a - b)2]
Do đó; c4 = (a2 - b2) 2
Suy ra a2 = b2 + c2 hoặc b2 = c2 + a2
Suy ra; tam giác ABC vuông tại A hoặc B.

TL:
sinA+sinB+sinC=1-cosA+cosB+cosC => Tam giác ABC Vuông tại A
Vế trái = sinA + sinB + sinC
= 2sin(A + B)/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2[cos(A - B)/2 + sinC/2]
=2.cosC/2.[cos(A - B)/2 + cos(A + B)/2]
= 4.cosC/2.cosB/2.cosA/2
Vế phải = 1 - cosA + cosB + cosC
= 2sin²A/2 + 2cos(B + C)/2.cos(B - C)/2
= 2.sinA/2[sinA/2 + cos(B - C)/2] (vì cos(B + C)/2 = sinA/2)
= 2.sinA/2[cos(B + C)/2 + cos(B - C)/2
= 4.sinA/2.cosB/2.cosC/2
Vậy sinA + sinB + sinC = 1 - cosA + cosB + cosC
<=> cosA/2.cosB/2.cosC/2 = sinA/2.cosB/2.cosC/2
<=> cosB/2.cosC/2(sinA/2 - cosA/2) = 0
mà cosB/2 ≠ 0 và cosC/2 ≠ 0
=> sinA/2 = cosA/2
<=> A/2 = 45o
<=> A = 90o
tam giác ABC vuông tại A

\(2sinB.sinC=1+cosA\Leftrightarrow cos\left(B-C\right)-cos\left(B+C\right)=1+cosA\)
\(\Leftrightarrow cos\left(B-C\right)+cosA=1+cosA\)
\(\Leftrightarrow cos\left(B-C\right)=1\)
\(\Rightarrow B-C=0\Rightarrow B=C\)
\(sinA=\frac{cosA+cosB}{sinB+sinC}=\frac{cosA+cosB}{2sinB}\) (do \(B=C\))
\(\Leftrightarrow2sinA.sinB=cosA+cosB\)
\(\Leftrightarrow cos\left(A-B\right)-cos\left(A+B\right)=cosA+cosB\)
\(\Leftrightarrow cos\left(A-B\right)+cosC=cosA+cosB\)
\(\Leftrightarrow cos\left(A-B\right)+cosB=cosA+cosB\)
\(\Leftrightarrow cos\left(A-B\right)=cosB\)
\(\Rightarrow A-B=B\Rightarrow A=2B=B+C\)
Mà \(A+B+C=180^0\Rightarrow2A=180^0\Rightarrow A=90^0\)
\(\Rightarrow\Delta ABC\) vuông cân tại A

Không mất tính tổng quát giả sử: \(A\ge B\ge C\)
=> \(tanA\ge tanB\ge tanC;cosA\le cosB\le cosC\)
Áp dụng BĐT Chebyshev ta có:
\(\left(\dfrac{tanA+tanB+tanC}{3}\right)\left(\dfrac{cosA+cosB+cosC}{3}\right)\ge\dfrac{tanA\cdot cosA+tanB\cdot cosB+tanC\cdot cosC}{3}\)
=> \(\dfrac{sinA+sinB+sinC}{cosA+cosB+cosC}\le\dfrac{tanA+tanB+tanC}{3}\)
mặt khác ta có: \(tanA+tanB+tanC=tanA\cdot tanB\cdot tanC\)
=> \(\dfrac{sinA+sinB+sinC}{cosA+cosB+cosC}\le\dfrac{tanA\cdot tanB\cdot tanC}{3}\left(đpcm\right)\)
đẳng thức xảy ra khi tam giác ABC đều
Đề sai.
\(tan90^o=\dfrac{1}{0}\) (không thể chia cho không) nên đề bài sai với trường hợp tam giác vuông rồi.


