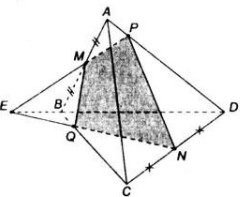
Cho tứ diện ABCD sao : AD = BC = a .Gọi M là điểm trên cạnh AB (M không trùng với
A và B) và N là điểm trên cạnh CD(N không trùng với C và D) sao cho: MA/AB+CN/CD = 1 .Gọi (P) là
mặt phẳng chứa MN và song song với BC .
a) Xác định thiết diện tạo bởi mặt phẳng (P) với tứ diệnvà tính chu vi của thiết diện theo a.
b) Chứng minh: AD // (P) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

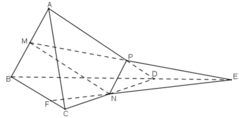
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

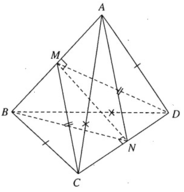
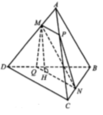
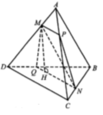
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.

a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành