Có những cặp số nguyên nào thỏa mãn x.y=x+y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 12 2015
1)
\(xy-y=x\Leftrightarrow y=\frac{x}{x-1}=1+\frac{1}{x-1}\)
y thuộc Z => x -1 thuộc U(1) ={ -1;1}
+x =-1 => y =0
+x =1 => y =2
2) \(x.\left(1-\frac{1}{7}\right)<1\frac{6}{7}\Leftrightarrow x.\frac{6}{7}<\frac{13}{7}\Rightarrow x<\frac{13}{7}.\frac{7}{6}=\frac{13}{6}=2,1\left(6\right)\)
x thuộc Z+ => x thuộc {1;2}
PT
1
ND
1
1 tháng 8 2016
x + y + xy = 2
=> x + y + xy +1 = 3
=> (x +1 ) + ( y + xy ) = 3 => ( x + 1).( y + 1) = 3
=> ( x +1) và ( y +1 ) thuộc Ư (3) ={ -3 ; -1 ; 1; 3 }
xét : x + 1 = -1 và y +1 = -3 => x = -2: y = -4
các con khác làm tương tự
18 tháng 1 2016
5=1.5=5.1=(-1).(-5)=(-5).(-1)
=> có 4 cặp
các bạn cho mk vài li-ke cho tròn 880 với
ND
6
NC
1
7 tháng 2 2020
x^2y -2x=5
x( xy-2)=5
Nếu x =1 và xy-2 =5
Suy ra x =1 và y=7
Nếu x = -1 và xy-2 = -5
Suy ra x = -1 và y=3
Tương tự bạn có thể làm lại với 2 TH rồi KL
TH3 : x = 5; xy-2 =1
TH4: x= -5 ; xy-2 = -1
8 tháng 2 2016
Câu này dễ mà bạn giải như vầy nè:
Ta có: 7 = 1*7=7*1=-1*-7=-7*-1
Ta có bảng sau:
| x+1 | 1 | 7 | -1 | -7 |
| y+2 | 7 | 1 | -7 | -1 |
| x | 0 | 6 | -2 | -8 |
| y | 5 | -1 | -9 | -3 |
Vậy (x,y) thuộc {(0,5);(6,-1);(-2,-9);(-8,-3)}
Sai thì thôi nhé bạn
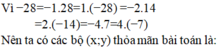
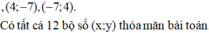
xy = x + y
<=> x(y - 1) - y = 0
<=> x(y - 1) - (y - 1) = 1
<=> (x - 1)(y - 1) = 1
Vì x; y nguyên => (x - 1) và (y - 1) cũng nguyên
Xét các hệ phương trình :
* x - 1 = 1 ; y - 1 = 1 <=> (x ; y) = (2 ; 2)
* x - 1 = -1 ; y - 1 = -1 <=> (x ; y) = (0 ; 0)
Vậy có hai cặp số (x;y) nguyên thỏa mãn phương trình là (2 ; 2) và (0 ; 0)
xy = x + y
<=> x(y - 1) - y = 0
<=> x(y - 1) - (y - 1) = 1
<=> (x - 1)(y - 1) = 1
Vì x; y nguyên => (x - 1) và (y - 1) cũng nguyên
Xét các hệ phương trình :
* x - 1 = 1 ; y - 1 = 1 <=> (x ; y) = (2 ; 2)
* x - 1 = -1 ; y - 1 = -1 <=> (x ; y) = (0 ; 0)
Vậy có hai cặp số (x;y) nguyên thỏa mãn phương trình là (2 ; 2) và (0 ; 0)