Cho M=3x4-8x3-6x2+8x+3.Phân tích biểu thức M thành nhân tử rồi tìm tất cả giá trị của x để M=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
a: \(=\left(2x-5\right)\left(4x^2+10x+25\right)\)

Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

1) \(\frac{3}{x^2-4y^2}\)
\(=\frac{3}{\left(x-2y\right)\left(x+2y\right)}\)
Phân thức xác định khi \(\left(x-2y\right)\left(x+2y\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x-2y\ne0\\x+2y\ne0\end{cases}}\Rightarrow x\ne\pm2y\)
2) \(\frac{2x}{8x^3+12x^2+6x+1}\)
\(=\frac{2x}{\left(2x+1\right)^3}\)
Phân thức xác định khi \(\left(2x+1\right)^3\ne0\)
\(\Rightarrow2x+1\ne0\)
\(\Rightarrow x\ne-\frac{1}{2}\)
3) \(\frac{5}{2x-3x^2}\)
\(=\frac{5}{x\left(2-3x\right)}\)
Phân thức xác định khi : \(x\left(2-3x\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x\ne0\\2-3x\ne0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x\ne0\\x\ne\frac{2}{3}\end{cases}}\)

Bài 1:
a: \(8x^3-2x=2x\left(4x^2-1\right)=2x\left(2x-1\right)\left(2x+1\right)\)
c: \(-5m^3\left(m+1\right)+m+1=\left(m+1\right)\left(-5m^3+1\right)\)

Bài 1: Ta có: \(A=1+4y-y^2=5-\left(y^2-4y+4\right)=5-\left(y-2\right)^2\le5\)
Dấu "=" xảy ra khi \(\left(y-2\right)^2=0\Rightarrow y-2=0\Rightarrow y=2\)
Vậy \(maxA=5\) khi \(y=2\)
Bài 2: Ta có: \(a^3+b^3+3ab=\left(a^3+3a^2b+3ab^2+b^3\right)-3a^2b-3ab^2+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b-1\right)=1-0=1\)

Chọn D
![]()
![]()
Hàm số có 2 điểm cực trị x 1 , x 2
![]()
Chia y cho y’ ta được :
![]()
Điểm cực trị tương ứng :
![]()
![]()
Với x 1 + x 2 = 4 x 1 x 2 = m + 2 nên y 1 y 2 = ( m - 2 ) 2 ( 4 m + 17 )
Hai cực trị cùng dấu ⇔ y 1 y 2 > 0
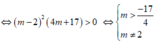
Kết hợp đk : - 17 4 < m < 2
\(M=3x^4-8x^3-6x^2+8x+3\)
\(=3x^4-12x^3+4x^3+9x^2+x^2-16x^2+12x-4x+3\)
\(=\left(3x^4-12x^3+9x^2\right)+\left(4x^3-16x^2+12x\right)+\left(x^2-4x+3\right)\)
\(=3x^2\left(x^2-4x+3\right)+4x\left(x^2-4x+3\right)+\left(x^2-4x+3\right)\)
\(=\left(3x^2+4x+1\right)\left(x^2-4x+3\right)\)
\(=\left(3x^2+3x+x+1\right)\left(x^2-3x-x+3\right)\)
\(=\left[3x\left(x+1\right)+\left(x+1\right)\right]\left[x\left(x-3\right)-\left(x-3\right)\right]\)
\(=\left(3x+1\right)\left(x+1\right)\left(x-1\right)\left(x-3\right)\)
M = 0\(\Leftrightarrow\left(3x+1\right)\left(x+1\right)\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow x\in\left\{\frac{-1}{3};-1;1;3\right\}\)