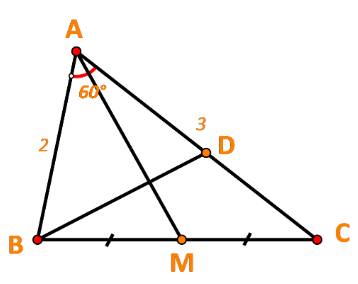
1/ Cho tam giác ABC có AB = 2, BC = 3 và \(\widehat{ABC}=60^o\)
a) Tính chu vi và diện tích của tam giác ABC.
b) Tìm vị trí điểm K sao cho \(\overrightarrow{KA}+\overrightarrow{KB}+2\overrightarrow{KC}=\overrightarrow{0}\).
c) Cho điểm M thay đổi nhưng luôn thỏa mãn \(\left(3\overrightarrow{MK}+\overrightarrow{AK}\right).\left(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\right)=0\). Chứng minh M luôn thuộc 1 đường tròn cố định.
2/ Giải phương trình và hệ phương trình:
a) \(\frac{\sqrt{5x-4x^2}-x}{x-1}=2\)
b) \(\left\{{}\begin{matrix}x^2-y=y^2-x\\x^2-6y=7\end{matrix}\right.\)