Cho tam giác ABC vuông tại A có BC=2AB. Tia phân giác của góc B cắt cạnh AC tại D. Gọi E là trung điểm của BC. Gọi F là giao điểm của tia ED và tia BA. CMR:
a) Tam giác ABD=tam giác EBD
b)DF=BC
c)Số đo các góc ABC,ACB,FDC tương ứng tỉ lệ với 2,1,4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABD và EBD CÓ
BD chung, góc abd= góc ebd, BE=BA
do dố tam giác abd= tam giác ebd (c-g-c)
b) vì tam giác ABD= tam giác EBD do đó
góc A= góc E (2 góc tương ứng)
mà góc A=90 nên góc E=90
=>DE vuông góc BC
c) Xét tam giác ADF và tam giác EDC có
AD=DE (TAM GIÁC ABD= EBD), GÓC A=GÓC E=90, HAI GÓC D BẰNG NHAU VÌ ĐỐI ĐỈNH
DO ĐÓ TAM GIÁC ADF= TAM GIÁC EDC
=>DF=DC (2 CẠNH TƯƠNG ỨNG )
MÌNH ĐÁNH CAPSLOCK THÔNG CẢM

a, Vì BD là tia phân giác của góc B suy ra:
góc ABD=góc EBD
Xét tam giác ABD và tam giác EBD có:
BA=BD(gt)
góc ABD=góc EBD(cmt)
BD chung
suy ra: tam giác ABD= tam giác EBD(cgc)
Vậy tam giác ABD= tam giác EBD
b,Vì tam giác ABD=tam giác EBD nên
góc BAD=góc BED(2 góc tương ứng)
mà góc BAD=90độ(tam giác ABC vuông tại A)
suy ra góc BED=90 độ
suy ra:DE vuông góc với BC
Câu c hình như đề bài sai

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
=>ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
c: Xét ΔBFC có
FE,CAlà đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc CF tại H
=>DH vuông góc CF tại H
mà ΔDFC cân tại D
nên H là trung điểm của FC
Xét ΔKFC có
CD là trung tuyến
CI=2/3CD
Do đó: I là trọng tâm
mà H là trung điểm của CF
nên K,I,H thẳng hàng

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE
và AK=EC
nên BK=BC

a) Hai tam giác = nhau theo trường hợp cạnh huyền góc nhọn (tự c/m)
b) Từ 2 tam giác = nhau ở phần a => AD= DE
Ta có tam giác ADF = tam giác EDC theo trường hợp góc cạnh góc (tự c/m)
=> DF= DC ( 2 cạnh tg ứng)
c) Xét tam giác ADF, có : góc A= 90 độ
=> DF là cạnh lớn nhất (quan hệ giữa góc và cạnh đối diện)
=> AD < DF
Mà DF= DC (chứng minh b)
=> AD < DC (đpcm)
b) Xét tam giác ADF và tam giác EDC, có:
Góc A= góc E (=90 độ)
AD= AE (vừa mình đã ns rồi)
Góc ADF= góc EDC (đối đỉnh)
Từ 3 điều trên => tam giác ADF = tam giác EDC (g-c-g)
=> DF= DC (2 cạnh tg ứng)

a. Hình vẽ (0.5 điểm)
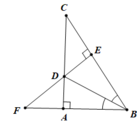
Xét ∆ABD và ∆EBD có:
∠(ABD) = ∠(DBE)
BD là cạnh chung
⇒ ∆ABD = ∆EBD(cạnh huyền – góc nhọn) (1 điểm)
a) Vì \(BC=2AB\left(gt\right)\)
=> \(AB=\frac{1}{2}BC\) (1).
Vì E là trung điểm của \(BC\left(gt\right)\)
=> \(EB=\frac{1}{2}BC\) (tính chất trung điểm) (2).
Từ (1) và (2) => \(AB=EB.\)
Xét 2 \(\Delta\) \(ABD\) và \(EBD\) có:
\(AB=EB\left(cmt\right)\)
\(\widehat{ABD}=\widehat{EBD}\) (vì \(BD\) là tia phân giác của \(\widehat{B}\))
Cạnh BD chung
=> \(\Delta ABD=\Delta EBD\left(c-g-c\right).\)
b) Phải là \(DF=DC\) nhé.
Theo câu a) ta có \(\Delta ABD=\Delta EBD.\)
=> \(AD=ED\) (2 cạnh tương ứng).
=> \(\widehat{BAD}=\widehat{BED}\) (2 góc tương ứng).
Mà \(\widehat{BAD}=90^0\left(gt\right)\)
=> \(\widehat{BAD}=\widehat{BED}=90^0.\)
Xét 2 \(\Delta\) vuông \(ADF\) và \(EDC\) có:
\(\widehat{DAF}=\widehat{DEC}=90^0\)
\(AD=ED\left(cmt\right)\)
\(\widehat{ADF}=\widehat{EDC}\) (vì 2 góc đối đỉnh)
=> \(\Delta ADF=\Delta EDC\) (cạnh góc vuông - góc nhọn kề).
=> \(DF=DC\) (2 cạnh tương ứng).
Chúc bạn học tốt!