Cho HS y=x^2-4x+4
Xác đinh toạ độ giao đỉnh và trục đx
Vẽ đồ thị HS trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2021
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
8 tháng 3 2022
a, bạn tự vẽ
b, Hoành độ giao điểm tm pt
\(x^2+x-2=0\)ta có a + b + c = 1 + 1 - 2 = 0
Vậy pt có 2 nghiệm x = 1 ; x = 2
Với x = 1 => y = -1
Với x = 2 => y = -4
Vậy (P) cắt (d) tại A(1;-1) ; B(2;-4)
31 tháng 3 2021
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Vậy: A(2;4) và B(-1;1)
KV
18 tháng 11 2023
a)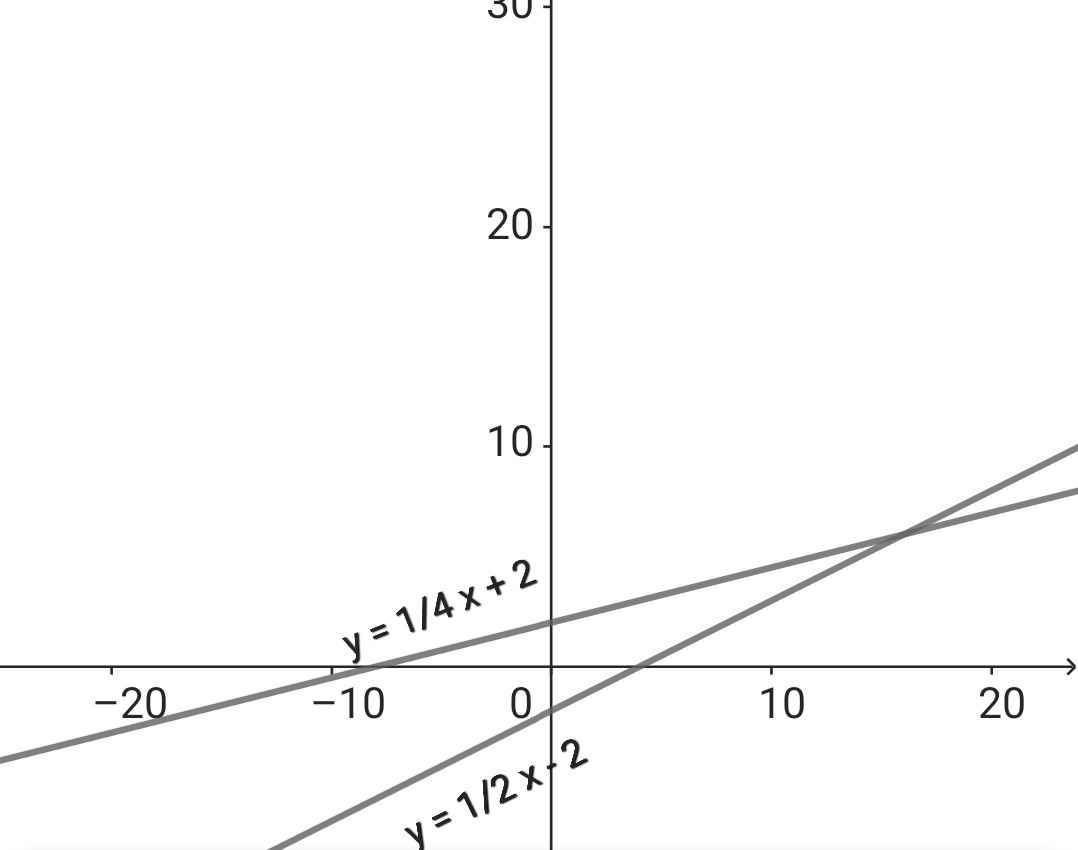 
b) *) Thay x = 0 vào (d) ta có:
y = 1/2 . 0 - 2 = -2
⇒ M(0; -2)
Thay x = 0 vào (d) ta có:
y = 1/4 . 0 + 2 = 2
⇒ N(0; 2)
Phương trình hoành độ giao điểm của (d) và (d)
1/2 x - 2 = 1/4 x + 2
⇔ 1/2 x - 1/4 x = 2 + 2
⇔ 1/4 x = 4
⇔ x = 4 : (1/4)
⇔ x = 16
Thay x = 16 vào (d) ta có:
y = 1/2 . 16 - 2 = 6
⇒ P(16; 6)
9 tháng 7 2023
a: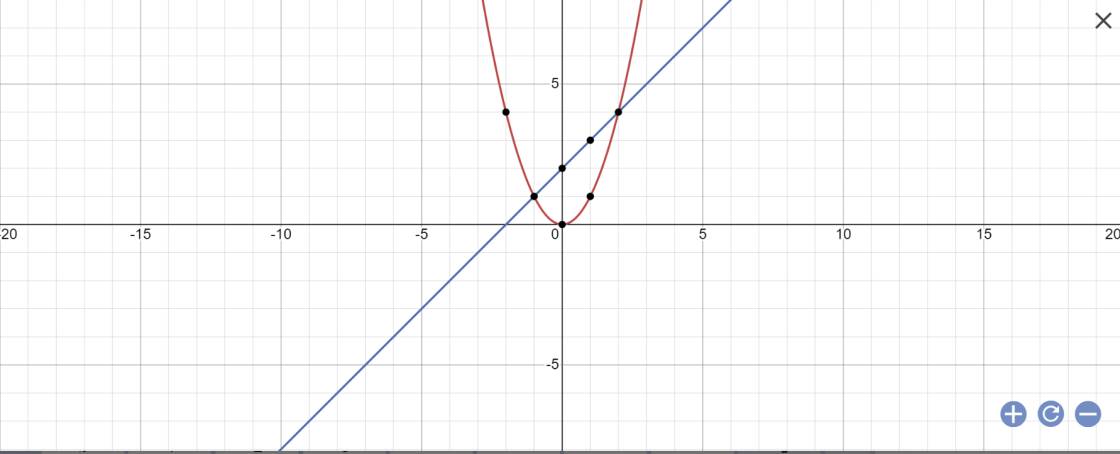 
b: PTHĐGĐ là:
x^2-x-2=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1