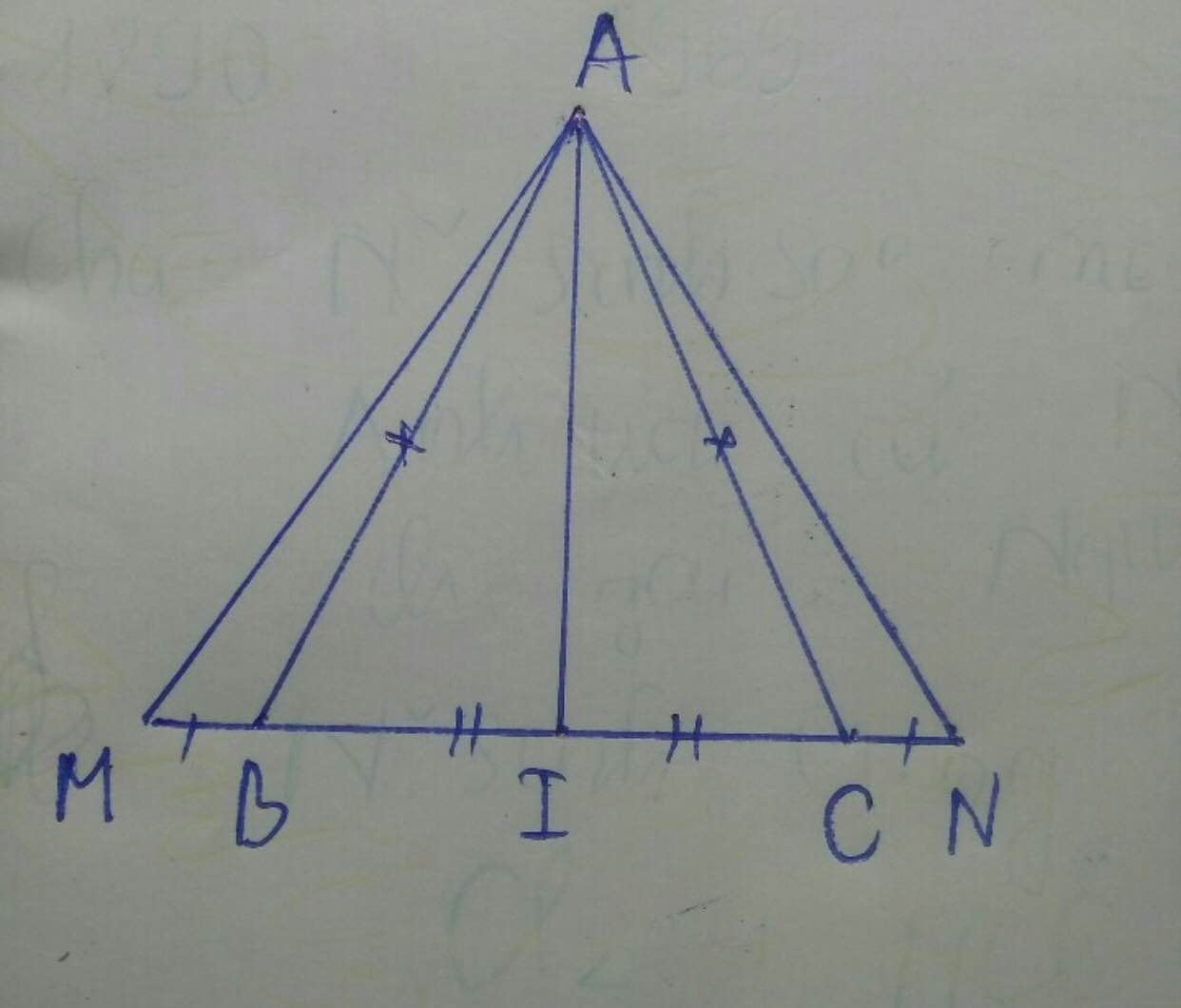
cho tam giác ABC với AB = AC . Lấy I là trung điểm BC. Trên tia BC lấy điểm N trên tia CB lấy điểm M sao cho CN = BM
a/ Chứng minh góc ABI = góc ACI và AI là tia phân giác góc BAC
b/ Chứng minh AM = AN
c/ Chứng minh AI và BC là hai đường thẳng vuông góc


a) Xét \(\Delta ABI\)và \(\Delta ACI\)có:
AB = AC (gt)
AI là cạnh chung
BI = CI (I là trung điểm của BC)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{ACI}\)(2 góc tương ứng)
\(\widehat{BAI}=\widehat{CAI}\)(2 góc tương ứng)
=> AI là tia phân giác của góc BAC
b) Xét \(\Delta ABM\)và \(\Delta ACN\)có:
AB = AC (gt)
\(\widehat{ABM}=\widehat{ACN}\)(cm a)
BM = CN (gt)
\(\Rightarrow\Delta ABM=\Delta ACN\left(c.g.c\right)\)
=> AM = AN (2 cạnh tương ứng)
b) Ta có: \(\Delta ABI=\Delta ACI\)(theo a)
\(\Rightarrow\widehat{AIB}=\widehat{AIC}\)(2 góc tương ứng)
Mà \(\widehat{AIB}+\widehat{AIC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{AIB}=\widehat{AIC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AI\perp BC\)
Vậy AI và BC là hai đường thẳng vuông góc
Hình tự vé nha bạn !!!
a) Xét tam giác vuông ABI và ACI ( ABI = 90 độ và AIC = 90 độ ) có :
AB = AC
BI = CI ( vì I là trung điểm của BC )
Suy ra Tam giác vuông ABI = Tam giác vuông ACI ( hai cạnh góc vuông )
Suy ra góc BAI = góc CAI ( 2 góc tương ứng )
BAI = CAI = \(\frac{BAC}{2}\)
Suy ra AI là tia phân giác góc BAC
Bạn làm phần a, trước đi nhé !!!
CHÚC BẠN HỌC TỐT !!