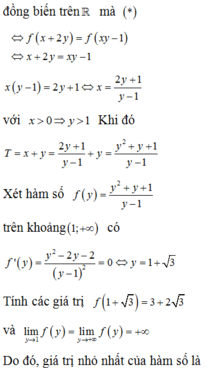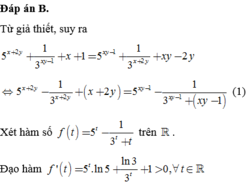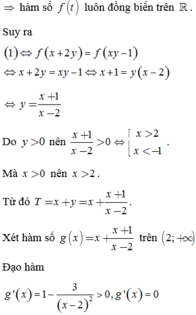tính giá trị nhỏ nhất của P=x^(3)+y^(3)+2x^(2)y^(2) biết x và y là các số thực thỏa mãn điều kiện:x+y=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 4 2021
\(K=\left(4xy+\dfrac{1}{4xy}\right)+\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\dfrac{5}{4xy}\)
\(K\ge2\sqrt{\dfrac{4xy}{4xy}}+\dfrac{4}{x^2+y^2+2xy}+\dfrac{5}{\left(x+y\right)^2}\ge2+4+5=11\)
\(K_{min}=11\) khi \(x=y=\dfrac{1}{2}\)
T
23 tháng 9 2019
\(P=\left(x+y\right)^3-3xy\left(x+y\right)+2x^2y^2\)
\(=2x^2y^2-3xy+1=2t^2-3t+\frac{5}{8}+\frac{3}{8}\) (đặt t = xy \(\Rightarrow t\le\frac{\left(x+y\right)^2}{4}=\frac{1}{4}\))
\(=\frac{1}{8}\left(4t-1\right)\left(4t-5\right)+\frac{3}{8}\ge\frac{3}{8}\)
Do đó \(P\ge\frac{3}{8}\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}x+y=1\\t=\frac{1}{4}\\x=y\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\)
True?
CM
26 tháng 4 2018
Đáp án B.
Từ giả thiết, suy ra
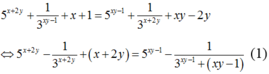
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
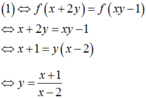
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
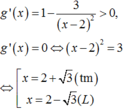
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
CV
16 tháng 6 2019
https://diendantoanhoc.net/topic/182493-%C4%91%E1%BB%81-thi-tuy%E1%BB%83n-sinh-v%C3%A0o-l%E1%BB%9Bp-10-%C4%91hsp-h%C3%A0-n%E1%BB%99i-n%C4%83m-2018-v%C3%B2ng-2/
CV
16 tháng 6 2019
bài này năm trrong đề thi tuyển sinh vào lớp 10 ĐHSP Hà Nội Năm 2018 (vòng 2) bn có thể tìm đáp án trên mạng để tham khảo
CM
27 tháng 3 2019
Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .