Question

[Vyly Hong]

Bài 1:(3 điểm).

a) Tìm giá trị của m để hàm số y = (m + 1)x + 2 là hàm số bậc nhất.

b) Tìm giá trị của m để đồ thị hàm số y = 2x + m – 1 cắt trục tung tại điểm có tung đôi

bằng 1.

c) Tìm điều kiện của m để hàm số y=(2m + 1)x - 5 luôn nghịch biến

Bài 2: (3 điểm) Cho hàm số bậc nhất y = (m - 1)x + 3.

a) Tìm giá trị của m để đồ thị của nó song song với đồ thị hàm số y=- 2x + 1

b) Cho m = 3, hãy vẽ đồ thị hàm số trên.

c) Đồ thị hàm số ở câu b) cắt trục tung tại A, cắt trục hoành tại B. Tính diện tích tam giác

OAB (đơn vị đo trên các trục tọa độ là cm) và tính góc tạo bởi đồ thị hàm số với trục Ox.

Bài 3: (1 điểm) Viết phương trình của đường thẳng có hệ số góc bằng 3 và đi qua điểm

P(1;2)

Bài 4 :(2 điểm) Cho hai hàm số bậc nhất :

y=[m-}}x+1

(1)

y= (2-m)x - 3 (2)

Với giá trị nào của m thì :

a) Đồ thị của các hàm số (1) và (2) là hai đường thẳng cắt nhau ?

b) Đồ thị của các hàm số (1) và (2) cắt nhau tại điểm có hoành độ bằng 4 ?

Bài 5:(1 điểm) Đường thẳng y= mx + (2m + 1) luôn đi qua một điểm cố định, tìm tọa độ

của điểm cố định đó.

Ai jup em với ạ mai phải nộp rồi huhu,😭😭😭😭🙏🙏🙏🙏🙏

Answer 1

[phạm trí dũng]

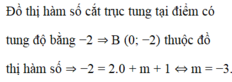
Bài1:
a,Để hàm số y=(m+1)x+2 là hàm bậc nhất
=>a≠0

=>m+1≠0
<=>m≠-1
Vậy m≠-1 thì đồ thị y=(m+1)x+2 là hàm bậc nhất.

Answer 2

[phạm trí dũng]

Bài 1:
b,Vì đồ thị y =2x+m-1 cắt trục tung tại diểm có tung độ =1
=>x=0;y=1
Thay x=0;y=1 vào y=2x+m-1
=>2.0+m-1=1
=>m=2
Vậy m=2 thì đồ thị y=2x+m-1 cắt trục tung tại điểm có tòa độ=1