cho a+b+c=1. Chứng minh a2+4b2+9c2\(\ge\frac{36}{49}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 2 2022
Đặt \(P=a+b+c\)
\(P^2=\left(a+b+c\right)^2=\left(1.a+\dfrac{1}{2}.2b+\dfrac{1}{3}.3c\right)^2\le\left(1^2+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2\right)\left(a^2+4b^2+9c^2\right)\)
\(\Rightarrow P^2\le\dfrac{49}{36}\left(a^2+4b^2+9c^2\right)=\dfrac{49}{36}\)
\(\Rightarrow-\dfrac{7}{6}\le P\le\dfrac{7}{6}\)
\(P_{min}=-\dfrac{7}{6}\) khi \(\left(a;b;c\right)=\left(-\dfrac{6}{7};-\dfrac{3}{14};-\dfrac{2}{21}\right)\)
\(P_{max}=\dfrac{7}{6}\) khi \(\left(a;b;c\right)=\left(\dfrac{6}{7};\dfrac{3}{14};\dfrac{2}{21}\right)\)
ND
0
NN
2
5 tháng 8 2023
\(\left(a-1\right)^2\ge0\Rightarrow a^2+1-2a\ge0\Rightarrow a^2+1\ge2a\left(1\right)\)
\(\left(2b-3\right)^2\ge0\Rightarrow4b^2+9-12b\ge0\Rightarrow4b^2+9\ge12b\left(2\right)\)
\(\left(c\sqrt[]{3}-\sqrt[]{3}\right)^2\ge0\Rightarrow3c^2+3-6c\ge0\Rightarrow3c^2+3\ge6c\left(3\right)\)
\(\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow a^2+1+4b^2+9+3c^2+3\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2+1+9+3\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2+13\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2\ge2a+12b+6c-13\)
mà \(2a+12b+6c-13>2a+12b+6c-14\)
\(\Rightarrow a^2+4b^2+3c^2>2a+12b+6c-14\)
\(\Rightarrow dpcm\)
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
A.
$a^2+4b^2+9c^2=2ab+6bc+3ac$
$\Leftrightarrow a^2+4b^2+9c^2-2ab-6bc-3ac=0$
$\Leftrightarrow 2a^2+8b^2+18c^2-4ab-12bc-6ac=0$
$\Leftrightarrow (a^2+4b^2-4ab)+(a^2+9c^2-6ac)+(4b^2+9c^2-12bc)=0$
$\Leftrightarrow (a-2b)^2+(a-3c)^2+(2b-3c)^2=0$
$\Rightarrow a-2b=a-3c=2b-3c=0$
$\Rightarrow A=(0+1)^{2022}+(0-1)^{2023}+(0+1)^{2024}=1+(-1)+1=1$
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
B.
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+y^2+6x+6y+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+9+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$ (do $y^2\geq 0$ với mọi $y$)
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
$\Rightarrow A_{\min}=2020; A_{\max}=2022$
CM
17 tháng 1 2018
Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c khác 0
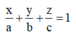
- Sử dụng bất đẳng thức
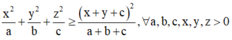
Đẳng thức xảy ra khi và chỉ khi
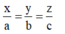
Cách giải:
Mặt phẳng (ABC) có phương trình:
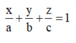
Khoảng cách từ O đến (ABC):
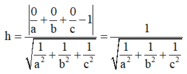
Ta có
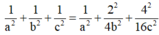
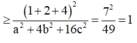
Dấu “=” xảy ra khi và chỉ khi:
CM
11 tháng 6 2017
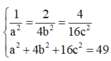
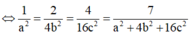
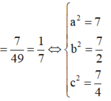
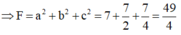
Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c khác 0): x a + y b + z c = 1
- Sử dụng bất đẳng thức: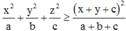 
Đẳng thức xảy ra khi và chỉ khi x a = y b = z c
Cách giải:
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c > 0)
Mặt phẳng (ABC) có phương trình: x a + y b + z c = 1
Khoảng cách từ O đến (ABC):
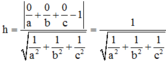
Ta có: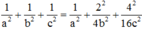 
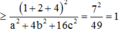
Dấu “=” xảy ra khi và chỉ khi:
=> 
HP
27 tháng 8 2021
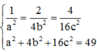
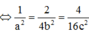
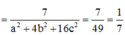
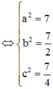
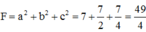
Giả sử \(c\le1\).
Khi đó: \(ab+bc+ca-abc=ab\left(1-c\right)+c\left(a+b\right)\ge0\)
\(\Rightarrow ab+bc+ca\ge abc\left(1\right)\)
Đẳng thức xảy ra chẳng hạn với \(a=2,b=c=0\).
Theo giả thiết:
\(4=a^2+b^2+c^2+abc\ge2ab+c^2+abc\)
\(\Leftrightarrow ab\left(c+2\right)\le4-c^2\)
\(\Leftrightarrow ab\le2-c\)
Trong ba số \(\left(a-1\right),\left(b-1\right),\left(c-1\right)\) luôn có hai số cùng dấu.
Không mất tính tổng quát, giả sử \(\left(a-1\right)\left(b-1\right)\ge0\).
\(\Rightarrow ab-a-b+1\ge0\)
\(\Leftrightarrow ab\ge a+b-1\)
\(\Leftrightarrow abc\ge ca+bc-c\)
\(\Rightarrow abc+2\ge ca+bc+2-c\ge ab+bc+ca\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\) Bất đẳng thức được chứng minh.
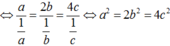
Lời giải:
Áp dụng BĐT Bunhiacopxky:
\((a^2+4b^2+9c^2)(1+\frac{1}{4}+\frac{1}{9})\geq (a+b+c)^2\)
\(\Leftrightarrow (a^2+4b^2+9c^2).\frac{49}{36}\geq 1\Leftrightarrow a^2+4b^2+9c^2\geq \frac{36}{49}\) (đpcm)
Dấu "=" xảy ra khi \(\frac{a}{1}=\frac{2b}{\frac{1}{2}}=\frac{3c}{\frac{1}{3}}\) hay $a=\frac{36}{49}; b=\frac{9}{49}; c=\frac{4}{49}$