Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AC và BC, K là một điểm trên đoạn BD, K không là trung điểm của BD. Tìm giao điểm của:
a)CD và (MNK)
b)AD và (MNK)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

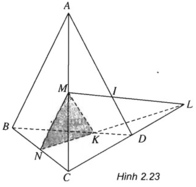
Nhận xét. Trên hình vẽ 2.23 không có sẵn đường thẳng nào của mặt phẳng (MNK) cắt AD. Ta xét mặt phẳng chứa AD chẳng hạn (ACD) rồi tìm giao tuyến ∆ của (ACD) với (MNK). Sau đó tìm giao điểm I của ∆ và AD, I chính là giao điểm phải tìm.
Gọi L = NK ∩ CD
Ta có L ∈ NK ⇒ L ∈ (MNK)
L ∈ CD ⇒ L ∈ (ACD)
Nên ML = (ACD) ∩ (MNK) = Δ
Δ ∩ AD = I ⇒ I = (MNK) ∩ AD

Đáp án B
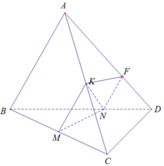
Xét (MNK) và (ABD) có:
N là điểm chung
AB // MK ⇒ A B ⫽ M N K
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua N và song song AB
d cắt AB tại điểm F cần tìm
Vì FN // AB ( cách dựng)
![]()

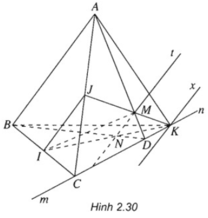
a)
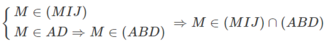
Ta cũng có:
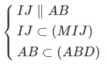
⇒ (MIJ) ∩ (ABD) = d = Mt và Mt // AB // IJ
b) Ta có: Mt // AB ⇒ Mt ∩ BD = N
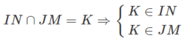
Vì K ∈ IN ⇒ K ∈ (BCD)
Và K ∈ JM ⇒ K ∈ (ACD)
Mặt khác (BCD) ∩ (ACD) = CD do đó K ∈ CD. Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. ( Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K.)
c) Ta có:
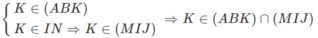
Mà
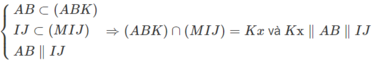

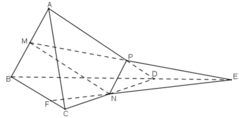
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

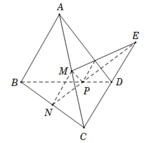
Chọn mặt phẳng phụ chứa CD là (BCD)
Do NP không song song CD nên NP cắt CD tại E
Điểm E ∈ N P ⇒ E ∈ M N P .
Vậy C D ∩ M N P tại E.
Chọn A

a) \(\left\{{}\begin{matrix}M\in\left(MIJ\right)\\M\in\left(AD\right)\Rightarrow M\in\left(ABD\right)\end{matrix}\right.\) \(\Rightarrow M\in\left(MIJ\right)\cap\left(ABD\right)\)
