Tam giác AbC vuông tại A , AB=2cm , AC=4cm . Khi đó độ dài cạnh AH bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2022
Xét \(\Delta AHC\left(\widehat{AHC}=90^o\right)\) có:
\(AC^2=AH^2+HC^2\) (định lí pitago)
\(\Rightarrow AH^2=AC^2-HC^2\)
\(\Rightarrow AH=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{AH^2}-\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}\)
\(\Rightarrow AB=3,75\left(cm\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC=\sqrt{3,75^2+5^2}=6,25\left(cm\right)\)
5 tháng 2 2022
\(AH=\sqrt{AC^2-HC^2}=3\left(cm\right)\)
\(HB=\dfrac{AH^2}{HC}=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=4+2,25=6,25(cm)
\(AB=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
27 tháng 12 2015
+) Ta có: AB vừa là đường cao vừa là đường trung tuyến
=> tam giác ADH cân tại A
=> AH = AD (1)
AC vừa là đường cao vừa là đường trung tuyến
=> tam giác AEH cân tại A
=> AH = AE (2)
Từ (1) và (2) => AH = AD = AE
+) Có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5cm\)
AH.BC = AB.AC
=> \(AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=\frac{12}{5}=2,4cm\)
+) Có: DE = AD + AE = AH + AH = 2AH = 2.2,4 = 4,8cm
Vậy DE = 4,8cm
VN
23 tháng 1 2017
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
VN
23 tháng 1 2017
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
22 tháng 4 2019
a, Xét tam giác HAB có: AB2 = AH2 + BH2 => AB2 = 42 + 22 => AB2 = 16 + 4 = 20 => AB = \(\sqrt{20}\)
Xét tam giác HAC có: AB2 = HA2 + HC2 => AC2 = 42 + 82 => AC2 = 16 + 64 = 80 => AC = \(\sqrt{80}\)
b, Ta có: AB < AC\(\left(\sqrt{20}< \sqrt{80}\right)\)
=>\(\widehat{B}< \widehat{C}\:\)(Quan hệ giữa cạnh và góc đối diện)
22 tháng 4 2019
Á mk nhầm nha \(\widehat{C}< \widehat{B}\)
#Hk_tốt
#Ngọc's_Ken'z
28 tháng 7 2015
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
CL
13 tháng 2 2016
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
LQ
7 tháng 1 2015
AB : |===|===|===|
AC: |===|===|===|===|
BC : |===|===|===|===|===| tổng 3 cạnh = chu vi = 2 cm
Cạnh AB có độ dài : 2 : 12 x 3 = 0,33 cm
Cạnh AC có độ dài : 2: 12 x 4 = 0,66 cm
Diện tích hình tam giác ABC là : 0,33 x 0, 66 : 2 = 0,1089 cm2
NẾU ĐỀ CHO CHU VI KHÁC THÌ LÀM TƯƠNG TỰ NHA. MÌNH THẤY CHU VI HÌNH NÀY NHỎ QUÁ !
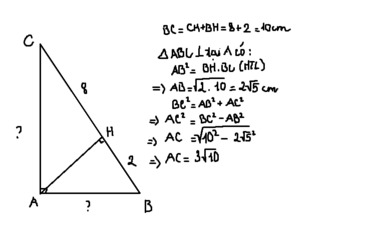
Áp dụng HTL:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\\ \Rightarrow AH^2=\dfrac{16}{5}\Rightarrow AH=\dfrac{4\sqrt{5}}{5}\left(cm\right)\)