Cho hình chóp S.ABCD. Điểm M lần lượt thuộc các cạnh BC và SD.
a) Tìm \(I=BN\cap\left(SAC\right)\)
b) Tìm \(J=MN\cap\left(SAC\right)\)
c) Chứng minh I, J, C thẳng hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Ta có:
\(\left. \begin{array}{l}M \in SA \subset \left( {SAC} \right)\\N \in SC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow MN \subset \left( {SAC} \right)\)
b) Ta có:
\(\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 12 2021
a.
Do O là tâm hbh \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow OJ\) là đường trung bình tam giác SAC
\(\Rightarrow OJ||SA\)
Mà \(SA\in\left(SAC\right)\Rightarrow OJ||\left(SAC\right)\)
\(SA\in\left(SAB\right)\Rightarrow OJ||\left(SAB\right)\)
b. O là trung điểm BD, I là trung điểm BC
\(\Rightarrow OI\) là đườngt rung bình tam giác BCD
\(\Rightarrow OI||CD\)
Mà \(CD\in\left(SCD\right)\Rightarrow OI||\left(SCD\right)\)
Tương tự ta có IJ là đường trung bình tam giác SBC \(\Rightarrow IJ||SB\Rightarrow IJ||\left(SBD\right)\)
c. Ta có I là trung điểm BC, O là trung điểm AC
\(\Rightarrow M\) là trọng tâm tam giác ABC
\(\Rightarrow BM=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{1}{3}\)
Theo giả thiết \(SK=\dfrac{1}{2}KD=\dfrac{1}{2}\left(SD-SK\right)\Rightarrow SK=\dfrac{1}{3}SD\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}=\dfrac{BM}{BD}\Rightarrow KM||SB\) (Talet đảo)
\(\Rightarrow MK||\left(SBC\right)\)
22 tháng 9 2023
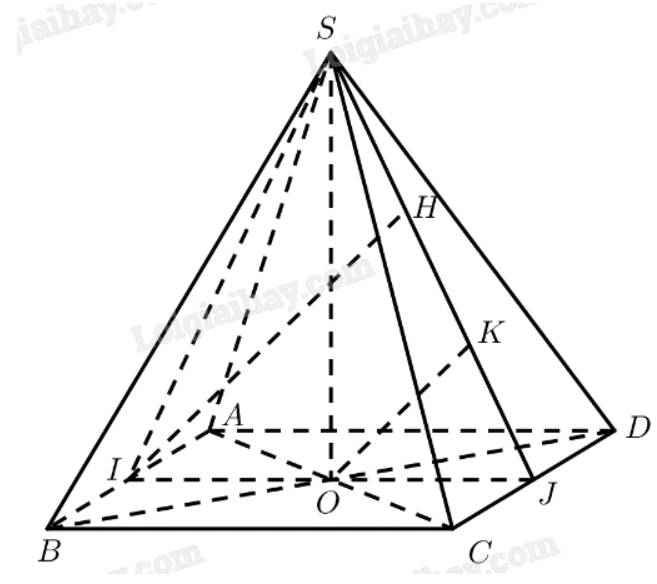
a) Gọi \(O\) là tâm của đáy
\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AB\)
\(I\) là trung điểm của \(AB\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow IJ\) là đường trung bình của hình vuông \(ABCD\)
\(\left. \begin{array}{l} \Rightarrow IJ\parallel A{\rm{D}}\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow IJ \bot AB\)
Ta có:
\(\left. \begin{array}{l}SO \bot AB\\IJ \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {SIJ} \right)\)
b) Kẻ \(IH \bot SJ\left( {H \in SJ} \right),OK \bot SJ\left( {K \in SJ} \right) \Rightarrow IH\parallel OK\)
\(O\) là trung điểm của \(IJ \Rightarrow IH = 2{\rm{O}}K\)
Ta có:
\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {AB,SC} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}\left. \begin{array}{l}AB \bot \left( {SIJ} \right)\\C{\rm{D}}\parallel AB\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SIJ} \right) \Rightarrow C{\rm{D}} \bot IH\\ & IH \bot SJ\end{array} \right\} \Rightarrow IH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {AB,C{\rm{D}}} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right) = IH\end{array}\)
\(O\) là trung điểm của \(IJ\), \(IH\parallel {\rm{O}}K\)\( \Rightarrow IH = 2{\rm{O}}K\)
\(O\) là trung điểm của \(B{\rm{D}}\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow OJ\) là đường trung bình của \(\Delta BCD\)
\( \Rightarrow OJ = \frac{1}{2}BC = \frac{a}{2}\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O\)\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \frac{{a\sqrt 6 }}{2}\)
\(\Delta SOJ\) vuông tại \(O\) có đường cao \(OK\)
\( \Rightarrow OK = \frac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }} = \frac{{a\sqrt {42} }}{{14}}\)
\( \Rightarrow d\left( {AB,C{\rm{D}}} \right) = IH = 2OK = \frac{{a\sqrt {42} }}{7}\)
25 tháng 5 2017
a) S, I, J, G là điểm chunng của (SAE) và (SBD)
b) S, K, L là điểm chung của (SAB) và (SDE)
30 tháng 10 2023
a: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình
=>MN//BD
BD//MN
\(MN\subset\left(AMN\right)\)
BD không thuộc mp(AMN)
Do đó: BD//(AMN)
b: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Chọn mp(SBD) có chứa MN
(SBD) giao (SAC)=SO(cmt)
Gọi K là giao điểm của SO với MN
=>K là giao điểm của MN với mp(SAC)
a/ Gọi O là giao điểm AC và BD
Trong mặt phẳng (SBD), nối SO cắt BN tại I \(\Rightarrow I=BN\cap\left(SAC\right)\)
b/ Nối MD cắt AC tại P
Trong mặt phẳng (SMD), nối MN cắt SP tại J
\(\Rightarrow J=MN\cap\left(SAC\right)\)
c/ Ba mặt phẳng (SAC); (BCN), (SDM) cắt nhau theo 3 giao tuyến phân biệt CI, MN, SP.
Mà SP cắt MN tại J \(\Rightarrow\) CI đi qua J hay C;I;J thẳng hàng