cho hàm số f(x) xác định với mọi x thỏa mãn f(X) +2f(1/x) = X^2 tính f(2019)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
IC
2
KN
22 tháng 11 2019
hàm số f(x) xác định với mọi x thỏa mãn \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\)nên:
+) x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=\frac{1}{9}\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=\frac{2}{9}\)(1)
+) x = \(\frac{1}{3}\)thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=9\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{-79}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{-79}{27}\)
KN
22 tháng 11 2019
Làm ngược, sửa:))
+) Nếu x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=9\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=18\)(1)
+) Nếu x = \(\frac{1}{3}\) thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=\frac{1}{9}\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{161}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{7}\)
20 tháng 3 2016
bài 1: f(x) + 2f(2-x)=3x (1)
f(2-x)+2[(2-(2-x)]=3(2-x) suy ra f(2-x)+2f(x)=6-3x suy ra 2f(2-x)+4f(x)=12-6x (2)
Lấy (2)-(1) ta có: 4f(x)-f(x)=12-6x-3x suy ra f(x)=4-3x
vậy f(2)=4-3*2=-2
Bài 2 tương tự: f(x)+3f(1/x)=x^2 (1)
f(1/x)+3f(x)=1/x^2 suy ra 3f(1/x)+9f(x)=3/x^2 (2)
Lấy (2)-(1) ta có: 9f(x)-f(x)=3/x^2-x^2 suy ra f(x)=(3-x^4)/8x^2
Vậy f(2)=(3-2^4)(8*2^2)=-13/32
CM
18 tháng 11 2017
Chọn C.
Ta có f ' x + 2 f x = 0 ⇔ f ' x = - 2 f x ⇔ f ' x f x = - 2 d o f x > 0
Lấy tích phân hai vế, ta được
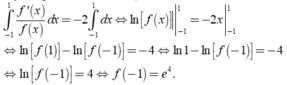
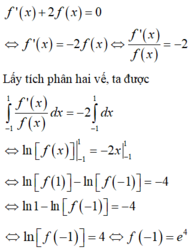
\(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\) (1)
\(\Rightarrow f\left(\frac{1}{x}\right)+2f\left(x\right)=\frac{1}{x^2}\Rightarrow2f\left(\frac{1}{x}\right)+4f\left(x\right)=\frac{2}{x^2}\) (2)
Trừ (2) cho (1): \(3f\left(x\right)=\frac{2}{x^2}-x^2\Rightarrow f\left(x\right)=\frac{2}{3x^2}-\frac{1}{3}x^2\)
\(\Rightarrow f\left(2019\right)=\frac{2}{3.2019^2}-\frac{1}{3}.2019^2\)