Bài 1: Từ tầng 9 của một tòa nhà, Nam thả rơi viên bi A. Sau 1s, Hùng thả rơi viên bi B ở tầng thấp hơn 10m. Hai viên bi sẽ gặp nhau lúc nào ( Tính từ khi viên bi A rơi ), g = 9,8 m/s2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
19 tháng 3 2019
Đáp án A
Chọn trục toạ độ thẳng đứng, chiều dương hướng xuống gốc toạ độ tại vị trí bạn Giang thả ở tầng 19, gốc thời gian lúc bi A rơi.
Phương trình chuyển động của viên bi A: với 
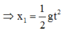
Phương trình chuyển động của viên bi B: với 
thả rơi sau 1s so vói gốc thời gian 
Khi 2 viên bi gặp nhau:
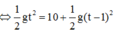
và cách vị trí thả của giang là
= 112,5m
VT
8 tháng 1 2018
Giải :
Chọn trục toạ độ thẳng đứng, chiều dương hướng xuống gốc toạ độ tại vị trí bạn Giang thả ở tầng 19, gốc thời gian lúc bi A rơi.
Phương trình chuyển động của viên bi A: với x 01 = 0 m ; v 01 = 0 m / s ⇒ x 1 = 1 2 g t 2
Phương trình chuyển động của viên bi B: với x 02 = 10 m ; v 02 = 0 m / s thả rơi sau 1s so vói gốc thời gian x 2 = 10 + 1 2 g ( t − 1 ) 2
Khi 2 viên bi gặp nhau: x 1 = x 2 ⇔ 1 2 g t 2 = 10 + 1 2 g ( t − 1 ) 2 ⇒ t = 1 , 5 s và cách vị trí thả của giang là x 1 = 1 2 g . t 2 = 1 2 .10.1 , 5 2 = 112 , 5 m
VT
18 tháng 3 2017
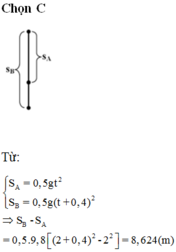
Chọn thời điểm viên bi A bắt đầu rơi làm mốc thời gian. Nếu gọi t là thời gian rơi của viên bi A thì thời gian rơi của viên bi B sẽ là t' = t + 0,5. Như vậy quãng đường mà viên bi A và B đã đi được tính theo các công thức :
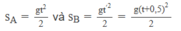
Từ đó suy ra khoảng cách giữa hai viên bi sau khoảng thời gian 2 s kể từ khi bi A bắt đầu rơi
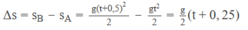
Suy ra ∆ s ≈ 11m
AT
1 tháng 3 2020
Thời gian hai viên bi gặp nhau là :
\(t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.10}{9,8}}=1,5s\)
VT
23 tháng 4 2018
a. Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :
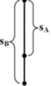
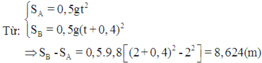
Chọn trục tọa độ thẳng đưgs, chiều dương hướng xuống.
Gốc tọa độ tại vị trí thả viên bi A.
Gốc thời gian là lúc viên bi A rơi.
Ptrình chuyển động:
+ Viên bi A: \(y_1=y_{02}+\dfrac{1}{2}gt^2=\dfrac{1}{2}gt^2\)
+ Viên bi B: \(y_2=y_{02}+\dfrac{1}{2}g\left(t-t_0\right)=10+\dfrac{1}{2}g\left(t-1\right)^2\)
Khi 2 viên bi gặp nhau thì: \(y_1=y_2\)
\(\Leftrightarrow\dfrac{1}{2}gt^2=10+\dfrac{1}{2}g\left(t-1\right)^2\)
\(\Leftrightarrow t=1,5s\)
Vậy.............