Cho hai đường tròn (O,R) và (O',R') cắt nhau tại A và B sao cho đường thẳng OA là tiếp tuyến của đường tròn (O',R'). Biết R=12cm,R'=5cm
a) CM: O'A là tiếp tuyến của đường tròn (O,R)
b) Tính độ dài các đoạn thẳng OO', AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PL
Phạm Lan Hương
17 tháng 11 2019
https://i.imgur.com/S0SmgZw.jpg
Đúng(0)
Những câu hỏi liên quan
CM
18 tháng 5 2017
(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’ 
ΔPBO
⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên:
O ’ P 2 = O ’ A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π . r 2 = 2 π ( c m 2 ) .
CM
28 tháng 2 2017
(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’ 
ΔPBO
⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên: O ' P 2 = O ' A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π · r 2 = 2 π cm 2
25 tháng 4 2017
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (o),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').
Hướng dẫn làm bài:
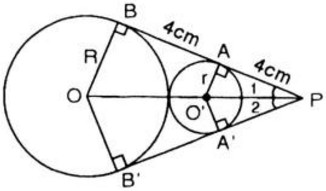
Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
ˆA=ˆB=900A^=B^=900
ˆP1P1^ chung
Vậy ΔOBP ~ ∆ O’AP
⇒rR=PO′PO=PAPB=48=12⇒R=2r⇒rR=PO′PO=PAPB=48=12⇒R=2r
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)
KD
25 tháng 4 2017
Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
chung
Vậy ΔOBP ~ ∆ O’AP
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)
21 tháng 1 2021
Gọi B', C' lần lượt là giao điểm khác A của AB, AC với (O').
Do BM, CM là tiếp tuyến của (O') nên ta dễ dàng chứng minh được:
\(BM^2=BA.BB'\); \(CM^2=CA.CC'\)
\(\Rightarrow\dfrac{BM^2}{CM^2}=\dfrac{BA.BB'}{CA.CC'}\). (1)
\(\Delta AOC\sim\Delta AO'C'(g.g)\Rightarrow \frac{AC}{AC'}=\frac{AO}{AO'}\).
Tương tự, \(\frac{AB}{AB'}=\frac{AO}{AO'}\).
Do đó \(\dfrac{AB}{AB'}=\dfrac{AC}{AC'}\Rightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Rightarrow\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\). (2)
Từ (1), (2) suy ra \(\dfrac{BM}{CM}=\dfrac{AB}{AC}\).
Theo tính chất đường phân giác đảo thì AM là đường phân giác ngoài của tam giác ABC
\(\Rightarrow\widehat{MAB}+\widehat{MAC}=180^o\Rightarrow180^o+\widehat{BAC}=2\widehat{EAC}\)
\(\Rightarrow180^o-\widehat{EAC}=\dfrac{180^o-\widehat{BAC}}{2}\). (3)
Các tứ giác FDEA, DBAC nội tiếp nên \(\widehat{FDB}=180^o-\widehat{EAC};\widehat{BDC}=180^o-\widehat{BAC}\). (4)
Từ (3), (4) suy ra \(\widehat{FDB}=\dfrac{\widehat{BDC}}{2}\) nên DF là phân giác góc BDC.