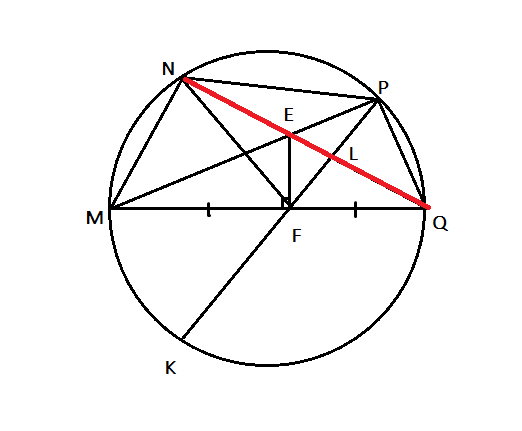
Cho tứ giác MNPQ nội tiếp (O) đường kính MQ, hai đường chéo MF và NQ cắt nhau tại E .Gọi F là điểm thuộc MQ sao cho EF vuông góc với MQ .Đường thẳng PF cắt (O) tại điểm thứ 2 là K. OQ và PF cắt nhau tại L . cmr :
a, tứ giác QEFP nội tiếp
b, FM là tia phân giác của góc NFK
c, EN.QL=QL.EL