trg 1 bảng ô vuông gồm có 5*5 ô vuông , người ta viết vào mỗi ô vuông chỉ một trg 3 số 1; 0 hoặc -1 . CMR : trg các tổng của 5 số theo mỗi cột , mỗi hàng , mỗi đg chéo phải có ít nhất hai tổng số bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1 2019
bài này cũng khá khó gặm but đối với anh thì khác!
Vì bảng ô vuông có kích thước 5x5 nên có tất cả:5 hàng,5 cột,2 đường chéo nên có tất cả 12 tổng.
Do khi điền vào các ô là các số 0,1,-1 nên mỗi tổng(S) là một số nguyên thỏa mãn:\(-5\le S\le5\)
\(\Rightarrow\)có 11 giá trị trong khi đó có 12 tổng nên theo nguyên lý Đi-rích-lê(hay còn gọi là chuồng thỏ) thì tồn tại ít nhất 2 tổng có giá trị bằng nhau.
Bài toán được chứng minh_._
1 tháng 4 2019
Vì bảng ô vuông có kích thước 5x5 nên có tất cả:5 hàng,5 cột,2 đường chéo nên có tất cả 12 tổng.
Do khi điền vào các ô là các số 0,1,-1 nên mỗi tổng(S) là một số nguyên thỏa mãn:−5≤S≤5
⇒có 11 giá trị trong khi đó có 12 tổng nên theo nguyên lý Đi-rích-lê(hay còn gọi là chuồng thỏ) thì tồn tại ít nhất 2 tổng có giá trị bằng nhau.
(ĐPCM)
16 tháng 4 2016
Giá trị nhỏ nhất của mỗi tổng là: -1 + -1 + -1 + -1+ -1 = -5
Giá trị lớn nhất của mỗi tổng là : 1+1+1+1+1=5
=> Số giá trị mà mỗi tổng có thể nhận được là : [5 - (-5) ] +1 = 11 giá trị
có 5 tổng theo hàng ngang, 5 tổng theo hàng dọc, 2 tổng theo hàng chéo
=> có tất cả 12 tổng nhận 11 giá trị
=> theo nguyên lý ĐRL thì có ít nhất 2 tổng bằng nhau
21 tháng 10 2019
b)Vì bảng ô vuông có kích thước 5x5 nên có tất cả:5 hàng,5 cột,2 đường chéo nên có tất cả 12 tổng.
Do khi điền vào các ô là các số 0,1,-1 nên mỗi tổng(S) là một số nguyên thỏa mãn:−5≤S≤5
\(⇒\)có 11 giá trị trong khi đó có 12 tổng nên theo nguyên lý Đi-rích-lê(hay còn gọi là chuồng thỏ) thì tồn tại ít nhất 2 tổng có giá trị bằng nhau.
21 tháng 10 2019
a)Nếu p chẵn => p=2 => p^2 + 2^p = 2^2 + 2^2 =8 (loại)
Nếu p lẻ :
+) p\(⋮\)3 => p=3 => p^2 + 2^p =17 (thỏa)
+)p ko chia hết cho 3. Đặt p=3k\(\pm\)1
p^2=(3k\(\pm\)1)^2=9k^2 \(\pm\)6k+1=3(3k^2 \(\pm\)2k)+1 chia 3 dư 1
Còn: 2^p\(\equiv\)(-1)^p\(\equiv\)-1 (mod 3) do p lẻ
Do đó:p^2+2^p=1+(-1)=0 (mod 3)
Mà p^2 + 2^p >3 nên ko thể là số nguyên tố (loại)
Vậy p=3 thì 2^p + p^2 là snt
DD
Đoàn Đức Hà
Giáo viên
28 tháng 5 2022
Trên mỗi hàng, mỗi cột phải có hai số -1, hai số 1.
Ta sẽ xếp theo hàng.
Ta có các khả năng của các hàng như sau:
(1) 1, 1, -1, -1
(2) 1, -1, -1, 1
(3) -1, -1, 1, 1
(4) -1, 1, -1, 1
(5) 1, -1, 1, -1
(6) -1, 1, 1, -1
Giả sử hàng 1 ta điền bộ (1). Ta có các trường hợp sau:
TH1: Hàng 2 điền bộ (1), khi đó hàng 3, hàng 4 ta phải điền bộ (3).
TH2: Hàng 2 điền bộ để tổng 2 số trong của các cột bằng 0, khi đó ta điền bộ (3). Hàng 3 và hàng 4 khi đó cũng phải điền sao cho tổng các cột trong hai hàng bằng 0. Có 6 cách điền như vậy.
TH3: Hàng 2 điền sao cho có 2 cột trong 4 cột có tổng bằng 0. Có 4 cách. Khi đó điền hàng 3 có 2 cách, điền hàng 4 có 1 cách. Tổng số cách là: 1.4.2.1=8 (cách).
Vậy có tổng số cách là: 6.(1 + 6 + 8) = 90 (cách).
CM
12 tháng 8 2017
Chọn B.
Cách giải:
Nhận xét: Để tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0 thì số lượng số 1 và số lượng số -1 trong mỗi hàng và mỗi cột đều là 2.
⇔ Mỗi hàng và mỗi cột đều có đúng 2 số 1.
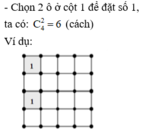
- Ở mỗi hàng mà chứa 2 ô vừa được chọn, ta chọn đúng 1 ô để đặt số 1, khi đó có 2 trường hợp:
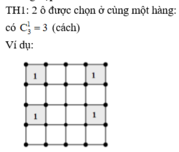
Khi đó, ở 2 hàng còn lại có duy nhất cách đặt số 1 vào 4 ô : không cùng hàng và cột với các ô đã điền. Như hình vẽ sau:
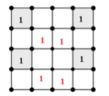
TH2: 2 ô được chọn khác hàng: có: 3.2 = 6 (cách)
Ví dụ:
Khi đó, số cách đặt 4 số 1 còn lại là: 1.1.2! = 2 (cách), trong đó, 2 số 1 để vào đúng 2 ô còn lại của cột chưa điền, 2 số 1 còn lại hoàn vị vào 2 ô ở 2 cột vừa điền ở bước trước. Ví dụ:
CM
23 tháng 4 2019
Đáp án A
Xét 1 hàng (hay 1 cột bất kì). Giả sử trên hàng đó có x số 1 và y số -1. Ta có tổng các chữ số trên hàng đó là x - y. Theo đề bài có x - y = 0 ⇔ x = y.
Lần lượt xếp các số vào các hàng ta có số cách sắp xếp là 3!.3!.2.1 =72 (Cách)