(x2 + x +1)(x2 - x + 1)(x4 - x2 +1)(x8 - x4 +1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HM
2
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Bạn cần viết đầy đủ đề: Bao gồm yêu cầu đề và công thức toán để được hỗ trợ tốt hơn.
26 tháng 8 2021
\(D=\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left[\left(x^2+1\right)^2-x^2\right]\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left(x^4+x^2+1\right)\left(x^4-x^2+1\right)\cdot\left(x^8-x^4+1\right)\)
\(=\left(x^8+2x^4+1-x^4\right)\left(x^8-x^4+1\right)\)
\(=\left(x^8+1\right)^2-x^8\)
\(=x^{16}+x^8+1\)
TB
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
a) \(\left(x+1\right)\left(x-1\right)\)
\(=x^2-1^2\)
\(=x^2-1\)
b) \(\left(x+1\right)\left(x-1\right)\left(x^2+1\right)\)
\(=\left(x^2-1\right)\left(x^2+1\right)\)
\(=\left(x^2\right)^2-1^2\)
\(=x^4-1\)
c) \(\left(x+1\right)\left(x-1\right)\left(x^2+1\right)\left(x^2+1\right)-x^8\)
\(=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)-x^8\)
\(=\left(x^4-1\right)\left(x^4+1\right)-x^8\)
\(=\left(x^4\right)^2-1-x^8\)
\(=x^8-1-x^8\)
\(=-1\)
26 tháng 8 2021
a: \(x^4+4=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
b: \(x^8+x^7+1\)
\(=x^8+x^7+x^6-x^6-x^5-x^4+x^5+x^4+x^3-x^3-x^2-x+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^6-x^4+x^3-x+1\right)\)
c: \(x^8+x^4+1\)
\(=\left(x^8+2x^4+1\right)-x^4\)
\(=\left(x^4-x^2+1\right)\cdot\left(x^4+x^2+1\right)\)
\(=\left(x^4-x^2+1\right)\left(x^2+1-x\right)\left(x^2+1+x\right)\)
CM
6 tháng 6 2019
Lời giải của các bạn đều thỏa mãn yêu cầu đề bài là phân tích đa thức thành nhân tử
10 tháng 9 2021
\(a,=x+x^2-x^3+x^4-x^5+1+x-x^2+x^3-x^4-x-x^2+x^3-x^4+x^5+1+x-x^2+x^3-x^4\\ =2x-2x^2+2x^3-2x^4\)
13 tháng 11 2021
2: \(=\dfrac{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}{-\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{-\left(x+y\right)\left(x^2+y^2\right)}{x^2+xy+y^2}\)
PT
1
CM
10 tháng 1 2017
Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 =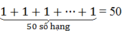 
Vậy giá trị đa thức bằng 50 tại x = -1.
PN
1
10 tháng 9 2021
\(=x+x^2-x^3+x^4-x^5+2+2x-2x^2+2x^3-2x^4-\left(1+x+x^2+x^3+x^4-x-x^2-x^3-x^4-x^5\right)\\ =2+3x-x^2+x^3-x^4-x^5-1\\ =-x^5-x^4+x^3-x^2+3x+1\)
DT
18 tháng 2 2022
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
18 tháng 2 2022
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
\(\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=[\left(x^2+1\right)^2-x^2]\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left(x^4+2x^2+1-x^2\right)\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left(x^4+x^2+1\right)\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=[\left(x^4+1\right)^2-x^4]\left(x^8-x^4+1\right)\)
\(=\left(x^8+2x^4+1-x^4\right)\left(x^8-x^4+1\right)\)
\(=\left(x^8+x^4+1\right)\left(x^8-x^4+1\right)\)
\(=\left(x^8+1\right)^2-x^8=x^{16}+2x^8+1-x^8=x^{16}+x^8+1\)